Тогда, как следует из формулы (1Л1), положение действительных собственных частот р. при известных значениях расчетных частот р1 будет определяться неравенствами

PfeK(l -)/(1+Ра) Pkpl У{\+Ш~)

(k= 1, 2, . . /г). (1.12)

Если все параметры системы определены содинаковой погрешностью ±3. причем IPI < 1, то с точностью до величин порядка

малости 6 имеем

рИ1-Р)<р<р1(1 + Р),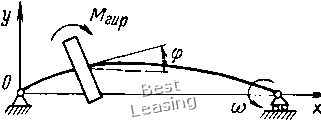

Рис. 1.2. Действие гироскопического момента в случае прямой прецессии вала

(1.13)

Т. е. погрешность определения собственных частот приближенно равна погрешности определения параметров системы.

Перейдем к определению погрешностей при расчете критических скоростей роторов.

Отличительными особенностями динамической системы ротор - опоры от рассмотренной выше являются наличие участков вала с распределенной массой и действие на систему гироскопических сил.

Первое отличие не является принципиальным, поскольку путем разбиения системы на достаточно большое число участков можно получить колебательную систему с конечным числом степеней свободы, совпадающую по динамическим свойствам с исходной системой с любой степенью точности.

Второе отличие заключается в следующем [30, 103]. Пусть диск, имеющий момент инерции относительно оси вращения А и экваториальный момент инерции 5, вращается вместе с валом с угловой скоростью (О (рис. 1.2). Под действием центробежных сил инерции, вызванных неизбежным дисбалансом центра масс диска, вал прогнется. Плоскость, в которой лежит изогнутая ось вала, будет совершать прецессионное вращение вокруг оси х также с угловой скоростью со. Если направление прецессии совпадает с направлением вращения вала, то такая прецессия называется прямой, если не совпадает - обратной.

Предположим, что в результате прогиба вала плоскость диска получает малое угловое отклонение ф. Тогда в случае прямой прецессии со стороны диска на вал будет действовать гироскопический момент [103 ]

Лгир - (Л -5)ф(o (1.14)

который стремится сделать вал более жестким. Критическая скорость примой процессии такого ротора будет больше, чем частота 10

свободных колебаний при о = 0. В случае обратной прецессий, наоборот, гироскопический момент стремится сделать вал более гибким, и критическая скорость уменьшается по сравнению с собственной частотой невращающегося вала.

В математическом плане, в случае произвольной роторной системы, учет гироскопического эффекта дисков приводит к появлению в дифференциальных уравнениях движения членов, содержащих первые производные от обобщенных координат по времени. Это приводит к структурному различию уравнения (1.3) и частотного уравнения роторной системы, так что к последнему не может быть применено преобразование (1.6).

Решение задачи по определению погрешностей может быть легко осуществлено, если использовать одно из свойств роторной системы, доказанное В. К. Дондошанским [33, с. 223]. Суть его заключается в следующем.

Критические скорости прямой и обратной прецессий ротора с учетом гироскопического эффекта дисков равны собственным частотам поперечных колебаний двух фиктивных невращающихся роторов, имеющих те же жесткостные и инерционные параметры, за исключением экваториальных моментов инерции дисков. Величины последних вычисляются по формулам:

для прямой прецессии Бфкт для обратной прецессии Бфикт

(1.15)

момент инерции того же диска относительно оси враще-его экваториальный момент инерции.

где А -ния; В

Очевидно, что поперечные колебания невращающегося ротора, представляющего собой обычную колебательную систему, могут быть описаны системой дифференциальных уравнений вида (1.1). Отсюда следует, что после замены действительных значений экваториальных моментов инерции дисков фиктивными по формуле (1.15) все полученные выше выражения по определению влияния погрешностей исходных данных на погрешности расчета собственных частот справедливы также и для критических скоростей роторов. Отличие состоит лишь в том, что предельная погрешность экваториальных моментов инерции дисков фиктивного ротора АВфи,,. вычисляется по формуле

фикт

А5 +АЛ,

где АБ и АЛ - предельные погрешности действительных моментов инерции.

Соответствующая относительная погрешность

= (ДБ + АЛ)/Б

фнкт*

(1.16)

Таким образом, погренлность определения критических скоростей роторных систем, вносимая неточностью исходных данных, может быть определена с помощью выражения (1.12). Учитывая

приближенную формулу (I.I3), можно заключить, что эта погрешность приблизительно равна погрешности определения жесткостных и инерционных параметров рассмотренной выше фиктивной роторной системы.

2. Виброактивность роторов двоякой жесткости

Одной из причин, вызывающих динамические нагрузки в опорах роторных машин с частотой, равной удвоенной частоте вращения, является наличие вала с неодинаковыми главными моментами инерции площади поперечного сечения.

Такие валы являются неравножесткими в различных плоскостях изгиба, т. е. обладают анизотропией жесткости. Так как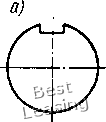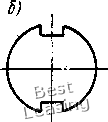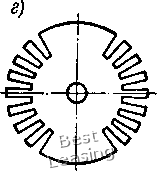

Рис. 1,3. Примеры поперечных сечений валов двоякойжесткости

В двух главных направлениях имеют место максимальная и минимальная жесткости, такие валы принято называть валами (роторами) двоякой жесткости.

Двоякая жесткость вала вызывается главным образом различного рода продольными вырезами: шпоночными канавками (рис. 1.3, а, б), срезами (рис. 1.3, в), пазами в цельнокованых роторах двухполюсных электрических генераторов (рис. 1.3, г) и. т. д.

Колебания роторов двоякой жесткости исследованы во многих работах. Наиболее подробно данный вопрос с обзором литературы по нему освещен в работах Ф. М. Диментберга [30], А. Тондла [100], А. Л. Цырлина [108]. В этих книгах исследуются различные проблемы, связанные с колебаниями роторов двоякой жесткости. В то же время в них отсутствуют данные по оценке уровня динамических нагрузок на опоры таких роторов.

В настоящем параграфе вначале приводятся основные качественные результаты, полученные в перечисленных работах, а затем исследуется вопрос о динамических нагрузках. В качестве теоретической модели рассматривается ротор с одним диском, закрепленным посередине невесомого горизонтального вала. Определение уровня динамических нагрузок производится как для случая абсолютно жестких шарнирных опор, так и для случая опирания вала на подшипники скольжения.

.14,-

Предположим, что исследуемый ротор представляет собой невесомый горизонтальный вал двоякой жесткости, несущий посередине диск массой т. Вал опирается на абсолютно жесткие шарнирные опоры; расстояние между опорами равно L (рис. 1.4, а).

Обозначим через /i и /g главные моменты инерции площади поперечного сечения вала, причем /а > /i- Соответствующие главные коэффициенты жесткости вала на изгиб:

q = 48£/i/L3; = 48EIJL,

Введем подвижную систему координат г], вращающуюся вместе с валом относительно неподвижной системы координат ху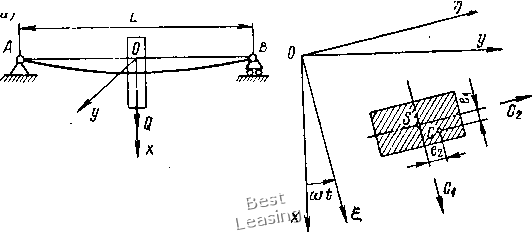

Рис. 1.4. Теоретическая модель ротора двоякой жесткости

с угловой скоростью (О, причем оси и г] направим вдоль главных осей инерции сечения (рис. 1.4,6). Пусть ех и - смещения центра масс диска относительно центра вала по осям й г); S - центр вала; С - центр тяжести диска; т - масса диска.

Дифференциальные уравнения движения центра тяжести диска во вращающейся системе координат получим, если кроме действующих на него силы упругости вала и силы тяжести приложим переносную и кориолисову силы инерции.

Проекции соответствующих сил на оси и г] составляют: силы упругости вала

силы тяжести

Ql = mg cos со/, = -mg sin (at;

переносной силы инерции

J, = mo)2( + ei), = m(o (tj + e);

кориолисовои силы инерции

Составив уравнения равновесия данной системы сил, изображенной на рис. 1.5, получим дифференциальные уравнения вида:

т [i - 2(дг\ - 0)2 + ех)] + Cil - mg cos со = 0; т [ц + 2(og - (й2(г] + ез) ] + сг\ + mg sin cof = 0.

Разделив уравнения (1.17) на m и введя обозначения

cjm = соь С2/т = coi,

получим следующие дифференциальные уравнения движения:

(I.I7)

2(0 т) 2(о

(со!

0)2)

eico + g COS (at;

((u2 - (0) T] = 2(0 - g" sin (at.

(1.18)

Общее решение уравнений (1.18) состоит из суммы трех решений; 1) общего решения однородной системы (1.18), описывающего свободные колебания; 2) частного решения неоднородной системы при ехфО, e2=h0 и mg = 0, соответствующего вынужденным колебаниям под действием эксцентриситета центра тяжести (случай вертикального ротора); 3) частного решения неоднородной системы при ji = 62 = О и mg ф О,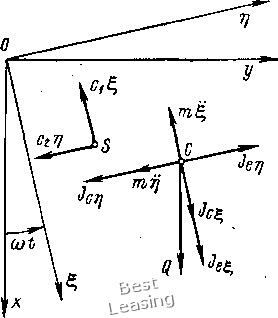

описывающего вынужденные колебания под действием силы тяжести диска.

Анализ общего решения однородной системы уравнений (1.18) показывает, что исследуемый ротор имеет две критические скорости, которые соответственно равны (Oi и (U2.

Зона частот вращения, лежащая между двумя критическими скоростями и CU2, является единственной областью неустойчивости. Следует отметить, что данная зона частот является областью параметрического резонанса, т. е. состояние неустойчивости возникает вследствие периодического изменения .жесткости системы в неподвижной системе координат.

Эксцентричное расположение центра тяжести диска вызывает круговое движение центра вала с частотой со и радиусом

!/ el (0) - 0)2)2 2 (2 0)2)2

Рис, 1,5. К выводу дифференциальных уравнений движения ротора двоякой жесткости

1е = <0

(0)f - 0)2) (0)2 0)2)

При (О -> И (О -* величина -» оо.

Остановимся подробнее на колебаниях системы под действием силы тяжести диска. Исходные дифференциальные уравнения получаются из (1.18) при = = О и имеют вид:

2ыг]

2(о1

- (со? - со) = g cos (at; (coi - со") ri = -gsin (at.

(1.19)

Частное решение неоднородной системы (1.19) отыскиваем в виде:

I = а cos (at; ц b sin (at, (1.20)

Подставив (1.20) в (1.19), получим следующие алгебраические уравнения относительно неизвестных а и Ь:

(со? - 2(а)а - 2(аЬ = g; -2(аа + (о)1 - 2(0) b -g.

Решая (1.21), находим:

g (0)1 - 40)2)

g (40)2 -0)2)

0)20)2 20)2 (0)2+0)1) 0)?0)1 - 20)2 (о)2 + ©2)

(1.21)

(1.22)

Введем комплексную величину

I + ir\ = а cos (at + ib sin (at,

которая может быть представлена в виде

t и ехр i(at + V ехр (-Ш),

(а + Ь):

(1.23)

1 . . f 4 1 - col -cof

o)fo)i-2o)(o)f+о))

1 / /. 1 o)f + 0)1 - 80)2

0-2-(a -0)--2 0)0)1-20)2(0)2+0)1) •

(1.24)

В неподвижной системе координат формула (1.23) принимает

вид или

2 = S ехр i(at = и ехр 2i(at + о X = а cos 2(oi + у; г/ = w sin 2(ui.

(1.25) (1.26)

Из формул (1.26) следует, что под действием веса диска центр вала движется по окружности радиуса и с частотой, равной удвоенной частоте вращения вала, а центр окружности смещен по вертикали на величину v.

Неограниченное возрастание амплитуды колебании и имеет

место при угловой скорости

0)fO)l

2 (0)2 + col)

2m (Ci + C2)

которую принято называть критической скоростью второго рода.