Жесткость подшйпникбвого узла при установке подшипника в опору с линейной жесткостью. Жесткостные характеристики подшипников качения, как видно из предыдущего, имеют сугубо нелинейный характер. Установка подшипника в опору с линейной жесткостью создает конструктивную систему с сочетанием линейных и нелинейных жесткостей.

Пусть радиальный шарикоподшипник установлен в опору с линейной жесткостью Ci. Подобную систему можно рассматривать как две последовательно соединенные пружины, а жесткость с узла в целом определится из соотношения

- -: - + - . (2.27)

Расчетная схема подобного подшипникового узла представлена на рис. 2.11, а, на рис. 2,11,6 - модель этой системы в виде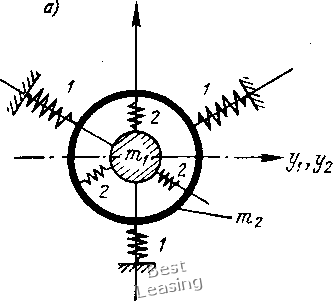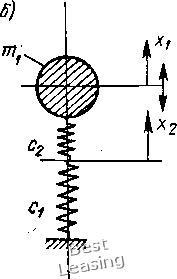

Рис. 2.11. Расчетная схема подшипникового узла: а - расчетная схема подшипникового узла в упругом линейном поле; б-динамическая модель ротора

с упругим шарикоподшипниковым узлом

Приведенной массы ротора и внутреннего кольца подшипника и двух последовательно соединенных пружин. Координаты и 2 соответствуют радиальным перемещениям внутреннего и наружного колец подшипника.

Если исходя из (2.15) представить относительное сближение колец шарикоподшипника как

)2/3

где Р - нагрузка на подшипник, то радиальная жесткость собственно подшипника

(2.28)

С другой стороны, Р = Cia, тогда можно Выразить радиальную жесткость Сг подшипника в функции от перемещения наружного кольца

f (х,) = К {СгХ,У\ (2.29)

Возвращаясь к (2.27) и учитывая (2.29), получим жесткость опоры в функции от радиального перемещения наружного кольца подшипника в упругой опоре

-. (2.30)

(Cl)

,-1/3-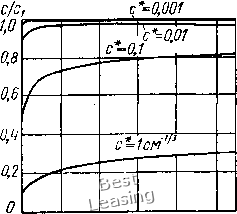

0,2 0,4 0,6 0,8 Wx,CM

Рис. 2Л 2. Изменение радиальной жесткости шарикоподшипника в упругой опоре в функции от радиального перемеш,ения наружного кольца подшипника (для различных значений жесткости упругой опоры)

Графики функций {с1с~ = / [х даны на рнс. 2.12 для трех значений параметра d {c-iflK, возрастающего с увеличением жесткости упругой опоры. Если для подшипников типа 200 и 206 коэффициент К соответственно равен 0,409 -10 и 0,746 • 10 кгс/см/ , то- при Ci = 500 1000 кгс/см параметр с будет

лежать в пределах (1,0ч-5) 10~см~-Из графика на рис. 2.12 видно» что в зоне малых перемещений жесткость опоры является нелинейной. Уменьшение жесткости упругой опоры уменьшает степень нелинейности

жесткости всего узла, причем суммарная жесткость узла с меньше жесткости упругой опоры с. Этот факт необходимо учитывать при расчете критических скоростей машины.

Аппроксимация нелинейной жесткостной характеристики подшипника степенным рядом. Восстанавливающая сила радиального шарикоподшипника определяется по выражению (2.22). В некоторых случаях, например при исследовании субгармонических колебаний в системах с шарикоподшипниками, можно для подшипника с нулевым предварительным натягом пользоваться для восстанавливающей силы более простым выралением, принимая за X абсолютную величину сближения колец подшипника,

Р (X) = Кх1\ (2.31)

которое все-таки неудобно для подстановки в уравнения движения ротора. Выражение (2.31) для приведения к более подходящему виду можно аппроксимировать степенным рядом

Р* {X)

(2.32)

Так как функция Р{х) должна быть симметрична относительно X, в (2.32) отсутствуют члены с четными степенями х. Ограничимся членом, содержащим х в третьей степени. Коэффициенты а

и b выбираются Из условия, минимизации квадратичного уклонения между Р (х) и аппроксимирующей функцией (х) на заданном интервале изменениял; от х до х.

[Р (X) ~. Р* (x)f dx = 0]

да .

дЬ J

Р {x)~P(x)fdx = 0.

(2.33)

Вычисляя интегралы (2.33) в пределах от О доЛ, и далее частг ные производные, найдем;

(2.34)

0,8 0,4 О

0,2 0,4 0,6 0,8 Г х,см

1,6 2,4А

Рис. 2.13. Аппроксимация нелинейной жесткостной характеристики шарикоподшипника:

; - исходная Р = Кх/\ 2 - аппроксн- мирующая Р = К (0,584л: -f 0,455.v3)

Рис. 2.14. Зависимость коэффициентов аппроксимирующей функции от амплитуды радиального перемещения внутреннего кольца подшипника

Если ожидаемый предел изменения х принять равным А = \, то аппроксимирующая функция примет вид

Р* {х) = 0,584Kx + 0,455Кх\ (2.35)

На рис. 2.13 сравниваются жесткостные характеристики (2.32) и (2.35) на интервале изменения х от О до 1. Коэффициенты а п Ь, вычисленные для различных пределов изменения х, характеризуют преобладание линейного или кубического члена в аппроксимирующей функции, а следовательно, и степень нелинейности системы. На рис. 2.14 показано изменение коэффициентов а п b с изменением амплитуды перемещений А. В области малых перемещений жесткостной параметр b при третьей степени л: значительно превышает параметр а. В области очень больших амплитуд параметр b можно считать малым, а систему - квазилинейной. 78

3. Динамика вала в псдшипниках качения

Динамическая модель и уравнения движения ротора.

Задача о движении ротора в подшипниках качения в совокупности всех факторов, влияющих на радиальную и осевую жесткость подшипника, сложна и требует решения на ЭВМ. Для аналитического исследования влияния наиболее существенных характеристик жесткости подшипника на динамику ротора примем ряд допущений, упрощающих расчетную схему.

Рассмотрим динамическую модель жесткого двухопорного ротора с центром тяжести, расположенным посередине ротора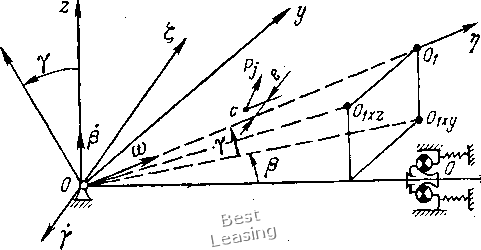

Рис. 2.15. Расчетная схема ротора в подшипнике с пружинным осевым предварительным натягом

(ротор симметричен). Одну из опор представим в виде жесткого шарнира, допускающего только угловые перемещения ротора, а вторую - в виде радиально-упорного шарикоподшипника с системой, обеспечивающей осевой предварительный натяг (рис. 2.15). При выводе уравнений движения ротора не будем учитывать периодических изменений жесткости подшипника, вызываемых прохождением шариков относительно вектора радиальной нагрузки на подшипник. Мощность источника вращения считается неограниченной.

Исходя из этого аналитическое исследование радиальных перемещений ротора проводится в настоящем параграфе в предположении, что жесткость подшипника функционально зависит только от относительных смещений колец подшипника. Принятое условие жесткости ротора означает, что при вращении ротора в абсолютно жестких опорах на всем диапазоне рабочих скоростей критическая скорость ротора лежит значительно выше рабочей зоны.

Будем учитывать при выводе уравнений только статическую неуравновешенность ротора, предполагая, что главная центральная ось инерции ротора параллельна его геометрической оси. Центр тяжести ротора смещен от геометрической оси на величину

эксцентриситета е. Положение шипа в подшипнике показано на рис. 2.16. Здесь О - геометрический центр опор; Oi - положение геометрической оси ротора и О - положение центра масс ротора с приложенной к нему силой инерции ротора Pj Месо, где М - масса ротора.

Выберем неподвижные оси координат xyz с началом в точке О и подвижные оси lt,r\ с началом в точке О. Выражение кинетиче-ской [энергии ротора, вращающегося вокруг неподвижной точки,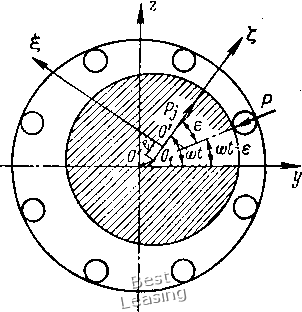

Здесь Je, Л, /,

(2.36) главные мо-

1 г\

менты инерции ротора.

Обозначим = J- В экваториальный момент инерции и Jy= А полярный момент инерции ротора вместе с подвижными частями подшипника; сое.

- проекции вектора

Рис. ".16. Положение шипа в шарикоподшипнике

угловой скорости ротора со на подвижные оси координат. Вычислим эти проекции с точностью до величин первого порядка малости, тогда;

р COS Y Р; (й - Т;

р sin у. (2.37)

В формулах(2.37) я у - углы между геометрической осью ротора и плоскостями хОг и хОу, Считая р и 7 малыми, можно положить р = г / и 7 = 2; , где / - расстояние между опорами. Учитывая (2.37), найдем окончательно выражение для кинетической энергии ротора

Т=1В {? + у) + А (cof2сой] .

(2.38)

Учтем в подшипнике сопротивление, пропорциональное первой степени скорости колебательного движения. Тогда диссипативная функция

n{z + y).

(2.3.9)

При принятых допущениях радиальное упругое поле подшипника можно считать изотропным. Тогда проекции нелинейной восста-

навливающей силы Р (г) на оси координат можно записать как Р (z) и Р (у). В результате для обобщенных сил имеем:

Q,= P{z)

МшвШо); coso).

(2.40)

Используя уравнение Лагранжа и считая А < В, приходим к дифференциальным уравнениям движения:

•

Введем новые обозначения:

Р (г) == Ме со sin 00; Р(у) =-Л1 (оЧоз 0).

(2.41)

"Б"

D; Ме

Я; P{z) = p(z); Р{у) = р{у)

Окончательтю получим уравнения вынужденных колебаний жесткого ротора с учетом линейных демпфирующих сил в подшипнике:

z + Dz + р (z) = Яо) sin 0); у + Dy + р (у) == Я(й cos (at.

(2.42)

Уравнения (2.42) не связаны между собой и их решения можно искать независимо друг от друга. В дальнейшем будем использовать для решения одно верхнее уравнение.

Ротор в подшипнике с нулевым предварительным натягом и зазором. При нулевом предварительном натяге и нулевом зазоре радиальную жесткостную характеристику подшипника можно представить в виде формулы (2.31). Для придания более удобного для подстановки в уравнения движения вида воспользуемся методом аппрсЗксимации. Коэффициенты полинома (2.34) в интервале Л от О до 2 будут: а - 0,827 К я b = 0,322К.

Подставив в уравнения движения (2.42) выражение для восстанавливающей силы в виде (2.32), получим

Я(й sin (x)t.

(2.43)

Введем безразмерную частоту и безразмерное время: