Тогда уравнение (2.43) примет вид

г + CsZ = ev sin vt,

d4 dz

dt dt

(2,44)

Будем искать решение с частотой возмущающей силы, полагая, что в районе резонанса преобладает основная гармоника

z = Лх sin vt + cos vt,

где Ai + А1 = /- - амплитуда ра-

г 2,0

диального перемещения ротора в подшипнике.

Подставив это выражение в исходное уравнение (2.44) и приравняв нулю коэффициенты при sin vt и cosvt, придем к уравнению I q \ а

3 22

1 -.v

0,5 . 1,0 1,5 2fi

Рис. 2.17. Амплитудно-частотная характеристика для ротора в шарикоподшипнике с нулевым предна-тягом

С помощью

(2.45) (2.45)

соотношения получим амплитудно-частотные характеристики рассматриваемой системы. На рис. 2.17 представлены амплитудно-частотные характеристики для t] - О и различных величин возмущающей силы. Неустойчивые части амплитудно-частотных кривых показаны тонкими линиями.

Более полный и строгий анализ колебаний ротора с учетом нелинейных свойств подшипника и нелинейного демпфирования дан в работах Э. Л. Позняка [82]. Задача ставится для вертикального ротора и горизонтального статически нагруженного. В постановке задачи учитывается радиальный зазор в подшипнике, но не рассматриваются безотрывные движения ротора. Восстанавливающая сила задается согласно закону Герца для шарикового подшипника и проектируется на координатные оси. Для вертикального ротора система уравнений движения записывается следующим образом:

2Fx = Me 0)2 cos 0); My + 2Fy = Meojsin coi, (2.46)

где Fx и Fy - проекции восстанавливающей силы и сил нелинейного демпфирования. Решение ищется методом гармонической

линеаризации. При этом форма движения ротора задается в виде круговой прецессии:

X = А cos{(ot + ф); у = Asin {(at + ф). (2.47)

Решение показывает, что для жесткого вертикального ротора амплитудно-частотные кривые носят резонансный характер, т. е. из-за податливости подшипников существует резонансный режим движения ротора, а сами амплитудно-частотные кривые имеют явно выраженный нелинейный вид, соответствующий системам с «жесткой» характеристикой.

Для горизонтального гибкого ротора с жестко закрепленцыми подшипниками решение ищется в виде суммы постоянных составляющих и гармоник основной частоты, так как в правой части уравнений движения имеются постоянные составляющие, появление которых, вызвано статической весовой нагрузкой, поэтому решение нельзя сводить к круговой прецессии. Исходные уравнения движения в этом случае имеют вид:

МхХх + Сх (Хх - х) = МхС(о cos (0t\

МгУх

М2Х2-

У2) = Мхе(а sin cat - Mxg]

М2У2

1 " .

Ci {Уг - i)

(2.48)

Здесь Мх - масса диска; - масса подшипников и приведенные к подшипникам массы частей вала; - жесткость вала; Fx и Fy определяются по формулам:

р (- - «

«12

(2,49)

где б - зазор в подшипнике; и - коэффициенты линейного и нелинейного демпфирования. Схема ротора, положение ротора в подшипниках показано на рис. 2.18.

Неизвестные амплитуды ищутся методом ортогонализации !81]. В результате показано, что резонансные скорости зависят от величины неуравновешенности и статической нагрузки. При этом критические скорости могут быть существенно меньше собственной частоты ротора на абсолютно жестких опорах. Увеличение зазора в подшипнике приводит к раздваиванию пика резонанса в горизонтальном и вертикальном направлениях; резо-нансы в горизонтальном направлении имеют место при меньших скоростях ротора, чем в вертикальном.

По сравнению с вертикальным ротором нелинейность системы со статически нагруженным горизонтальным ротором выражена

6* 83

в амплитудно-частотных характеристиках значительно слабее, а срывы и затягивания амплитуд имеют место лишь для гибких и сильно нагруженных роторов.

Снижение критической скорости ротора на подшипниках качения объясняется влиянием податливости собственно подшипника. Квазистатическая жесткость одного подшипника ищется из зависимости Р = Krl- при дифференцировании по г

dP 3 ,.2/3 nV3

(2.50)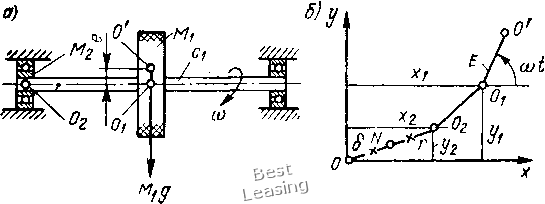

Рис. 2.18. Схема расположения ротора в подшипниках: а - расчетная схема гибкого ротора в шарикоподшипниках; б - положение центра диска, центра масс и оси ротора относительно центра опоры

Если не учитывать массу М, то Р = OSMg и первая критическая частота Qq найдется из выражения

27 16

27 16

(2.51)

где V -= Ке11сх\ а = M-igl{cxe)

В качестве примера сравниваются расчетные и экспериментальные данные для установки с ротором весом 700 кгс, опирающимся на радиальные шарикоподшипники 320 с числом шаров i = 8, с/щ - 36,5 мм и радиальным зазором 66-102 мкм. Вычисленная по формуле (2.50) квазистатическая жесткость при нагрузке, равной 1/2 веса ротора, = 0,24 10* кгс/см. Собственная частота ротора в жестких подшипниках составляет Q«, = 2130 1/с (20 300 об/мин). Расчетная же частота в опорах с коэффициентом жесткости оказалась равной 760 1/с (7240 об/мин). Для подшипника 320 коэффициент пропорциональности в формуле Герца К = 3,2.10** кгс/см-/ q 5 а 0,1 и отношение статической деформации в подшипнике к эксцентриситету rje = 2,64-4,0. Распределенная по длине неуравновешенность оценивалась в пределах е 25 мкм. Жесткость ротора определялась как q = MlQL = 3,15-10 кгс/см. Эксперимент

показал, что несмотря па различия в экспериментальном роторе и расчетной схеме, снижение критической частоты системы до /ifl 7500 об/мин действительно имело место. Также наблюдалось и некоторое раздваивание критических частот по вертикали и горизонтали.

Ротор в подшипнике с предварительным осевым натягом.

Рассмотрим случай вращения ротора в подшипнике с предварительным осевым натягом и с радиальной жесткостной характеристикой, описываемой выражением (2.12). Уравнение вынужденных колебаний ротора можно записать следующим образом:

г + -Ог -f 0) {k + z)

14 (гж-) (26 - г) - (26 - г) sin {(ot - г) Н(о sin со/.

(2.52)

Здесь col

собственная частота колебаний системы ро-

тор-осевая пружина; Pl/B - относительное усилие предварительного осевого натяга.

Чтобы найти периодическое решение нелинейного уравнения (2.52), воспользуемся методом гармонического баланса [17].

Введем в исходное уравнение (2.52) новую *1еременную и будем искать решение в виде

Z - А sin9. (2.53)

Тогда подстановка решения (2.53) в уравнение (2.52) приведет к следующим зависимостям:

Ло) = Н(а cos 8; 1. = Н(и sin s.

(2.54)

В выражении (2.54) Ii и определяются интегралами:

Р (Л 51пф)31Пфф;

/ (Ло) cos ф) cos ф с/ф Deo л.

(2.55)

В этих интегралах функция Р (Л sin ф) получена после подстановки в выражение (2.26) для восстанавливающей силы решения г Л sin ф, а функция / (Лео cos ф) Deo Л cos ф. Интеграл 1 при зычислении распадается на три интеграла:

(k-\- А sin ф) sin ф

4 гж

с/ф;

(26 - А sin ф) - (26 - Л sin ф)

{k-\- A sin ф) sin ф йф = (ОдЛ;

sin Ф с(ф ==

Для отыскания первого интеграла подынтегральную функцию разложим в биноминальный ряд, сходящийся при А < 26:

2 2" 2

2S f /(Л51пф)51пфф=:25 -

ak sin ф с/ф о

к + ak) А J sin ф ф + («2 + аз) Л" J sin ф ф о о

2л • / 2я -

(Ъ + «4) j Sin* Ф ф + (а -f ag) Л* [ sin ф ф о о

= 2(olS [(«1 + ak) Л + А лз (аз + ай)

Здесь а, «2» оз» «4 и - коэффициенты разложения, определяющиеся по формулам:

2S (аз + ak) =

2S(ai + ak) = 2 2

(-1) 2A.- 1 (2X- 1)3

(2.56)

462 (2-1)2 .

В уравнения (2.56) введен безразмерный параметр

б

характеризующий соотношение между радиальным зазором и геометрическими константами подшипника. С учетом полученных решений можно записать

/1 = 0)a2S (az + a2k) А + (al -- S (аз + щк) А ~ (аА + qo, - (2.57)

В результате имеем систему уравнений, связывающих амплитуду и фазовый угол с частотой возмущающего усилия.

(al2S (ai + ak)A-(al~S (аз + ak) А - ш1А

qo - Ло)2 = Н(а cos е; DcoA = Яй)2 sin 8.

(2.58)

Приведем уравнения (2.58) к более простому виду, решив их относительно е, для чего преобразуем исходные уравнения:

/1 - Лео = 1/"Яо) - ih tg 8 = h/{h - Ло)).

(2.59)

Коэффициентам при Л и.Л для сокращения записи присвоим новые обозначения:

(e-l) = 2S(ai + a,A); %

1 3 е/ = -2" S (аз

ak). (2.60)

Параметры 0 и % постоянны и определяются геометрическими соотношениями в подшипнике. Введем безразмерные величины: - 0)/сйд - безразмерная частота; i = Л/26 - безразмерная амплитуда; = /(260)2) = Ро/{а) - безразмерный натяг; ц = = D/o)a - безразмерный коэффициент демпфирования и h = Я/26 - безразмерный дисбаланс. Учитывая соотношения (2.60), приведем уравнения (2.59) к окончательному виду:

tg е

(2.6.1)

1 \2

Анализ решений нелинейных уравнений движения ротора в подшипниках с предварительным осевым натягом. Для идеально сбалансированного ротора h ~ О и без учета демпфирования решение (2.61) будет

9 + У).

(2.62)

Последнее выражение представляет собой уравнение скелетной кривой. Ряд подобных кривых для трех значений безразмерного натяга (v = 0; 0,5; 5,0) при постоянном значении параметра А. = 18 представлен на рис. 2.19. Параметр X рассчитан для подшипника 204 с радиальным зазором 6 = 2,5-10"® мм. После вычисления постоянных 0 и X имеем

QI = 17 + 8,6 + v,/

Согласно этому выражению и построены скелетные кривые на рис. 2.19. Без учета уменьшения натяга центробежными силами шариков значение безразмерного натяга в радиально-упорных подшипниках может в десятки раз превосходить значение параметра X. Например, для подшипника 204 при = 7,2 кгс натяг Vq = 280. Скелетные кривые для больших величин относительного натяга (vo,== 100; 50 при Я- = 1 и 18) построены на рис. 2.20. Как видно из рис. 2.19 и 2.20, при увеличении безразмерного натяга происходит смещение зоны безразмерных резонансных