частот в сторону их повышения. Однако безразмерная частота Qa = (о)/(йа) = 2В(ху1{1Са). Слсдовательно, зона резонансных частот реального ротора зависит от его геометрических и массовых характеристик, а также от жесткости осевой пружины. Изменения X, а значит и радиального зазора в подшипнике незначительно влияют на характер процесса, изменяя крутизну скелетной кривой.

Определим максимально возможные величины амплитуд при наличии демпфирования. Так как выражение под корнем в правой части первого уравнения системы (2.61) не может быть отрица-

тельным, необходимо ;fвыполнение неравенства

W 50S2b

200 500511

Рис. 2.19. Скелетные кривые ротора в шарикоподшипнике серии 204 с радиальным зазором S = 2,5 10~ мм

Рис. 2.20. Скелетные кривые ротора вшарикоподшипнике с большими усилиями предварительного осевого натяга:

/ Vo = 50; Я, = 1; 2 - ло = 50; Л 18; 5 - Vo= W\ = 1

Отсюда получим выражение, определяющее условие существования резонансного режима в системе с возмущающим усилием, пропорциональным квадрату частоты,

I iSla) < лад. (2.63)

Точка пересечения скелетной жривой и линии (2.63) определит максимально возможную амплитуду при данной безразмерной неуравновешенности ротора h и демпфировании г)). На рис. 2.21 представлены амплитудно-частотные характеристики для Я. = 1, Vo = 50 и трех значений h 0,1; 0,2; 0,3. Точки Л, и А определяют максимальные амплитуды при = 0,10; 0,05 и 0,033.

Рассмотрим устойчивость ветвей амплитудно-частотных характеристик, для чего воспользуемся методом бифуркаций, изложенным в [4].

Зависимость (2.61),- представленная без учета демпфирования в виде

Vo • -/г

a = 0,

Описывает положейие равновесия на плоскости параметров и йд. Практически эти положения реализуются лишь в случае их устойчивости. Каждому положению равновесия консервативной системы соответствует определенное состояние равновесия на фазовой плоскости, поэтому устойчивость равновесных положений зависит от характера особых точек, меняющегося при переходе через так называемые точки бифуркации, В точках бифуркации для данного случая

Д(, а) - о и /Ь(, йа) + 0.

На рис. 2.22 дана диаграмма устойчивости, построенная для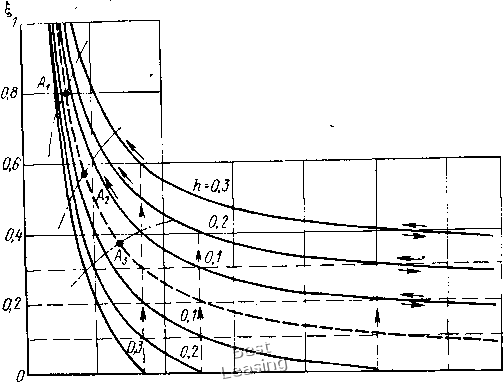

300 Ш 500 600 Sla

Рис. 2.21. Амплитудно-частотные характеристики ротора в шарикоподшипнике с предварительным осевым натягом (Я - 1,

Vo - 50):

At - ft/л = 0,1: Ai - 0,05; - 0,033

амплитудно-частотной характеристики. На этой диаграмме точками бифуркации являются точки М и Р, Точки, где (, Qa) = = О и (I, Qa) = О, также являются бифуркационными, но в них происходит изменение числа состояний равновесия (точка К)-Кривая равновесных положений /(, Qa) делит плоскость Q на области, в которых / (, Qa) < О, и на зону, где / (, Qa) > 0. На участке ОК положения равновесия устойчивы, так как на этом участке усилие предварительного натяга осевой пружины превышает осевые усилия, передающиеся через шарики со стороны ротора, и ротор не совершает гармонических движений, а амплитуда его колебаний равна нулю (в пределах принятых допущений об идеальности геометрии подшипника). В точке К ветвь ОК сливается с ветвью MKj а так как при изменении параметра Qa состояния равновссия на фазовой плоскости исчезают и появляются только парами, то ветвь КМ является неустойчивой. В этом случае на ветви ОК производная Д (I, Qa) > О, значит

в зоне, лежащей над ветвью ОК и ограниченной кривыми К/С и LL, функция / (I, Од) > 0. На рисунке эта зона заштрихована. Точки участков кривых, лежащих над заштрихованной областью, соответствуют устойчивым движениям ротора (выделены жирной линией). Точки участков кривых, лежащих под этой областью, соответствуют неустойчивым движениям ротора (тонкая линия).

Исходя из произведенного анализа можно сделать вывод, что ветви амплитудно-частотной характеристики, лежащие ниже скелетной кривой (см. рис. 2.21), являются неустойчивыми и при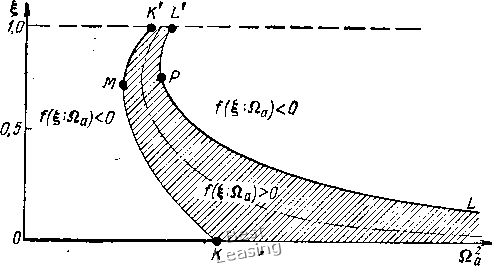

Рис. 2.22. Бифуркационная диаграмма устойчивости для ротора в шарикоподшипнике с преднатягом

разгоне ротора должен произойти скачок амплитуды на верхнюю устойчивую ветвь. Возвращаясь к рис. 2.17 (подшипник с нулевым натягом), отметим, что здесь скачок амплитуды будет не при разгоне, а при выбеге ротора. При разгоне же будет наблюдаться «затягивание» амплитуды в зону высоких частот.

Можно воспользоваться нелинейными свойствами шарикоподшипника с предварительным осевым натягом и, подобрав необходимый натяг, проходить зону резонанса без значительного увеличения амплитуды колебаний ротора. Подшипник в данном случае будет играть роль регулятора колебаний (аналогично демпферу сухого трения). При расчете натяга, необходимого для перехода через зону резонанса, следует учитывать уменьшение натяга центробежными силами шариков.

Уравнение скелетных кривых (2.62) с учетом центробежных сил шариков

l = 0 + + (Vo - от.) \ . (2.64)

Здесь <т - безразмерный параметр, определяемый конструктивными параметрами подшипника,

а центробежная сила для одного шарика Рц подсчитывается по формуле (2.9).

На рис. 2.23 построены скелетные кривые с учетом центробежных сил шариков для подшипника с параметрами Э = 17,0, X 8,6, а = 1 и ряда значений .безразмерного натяга Vq. Скелетная кривая, построенная для Vo - -5, характеризует работу вала в подшипнике с отрицательным натягом (зазором). Сравнивая кривые на рис. 2.21 и 2.23, можно заметить, что центробежные силы шариков уменьшают зону неустойчивости под скелетной кривой, а в случае малых натягов эта зона отсутствует вовсе,

0,2 О

Рис. 2.23. Скелетные кривые ротора в шарикоподшипнике с преднатягом с учетом центробежных сил шариков (штриховая линия объединяет точки с вертикальными касательными)

Следовательно, для перехода через резонансную зону потребуется больший натяг, причем для каждого безразмерного дисбаланса h потребуется своя минимальная величина v, при которой такой переход возможен. Аналитически условие, при выполнении которого осуществим переход через резонанс, выразится формулой

v>

{o + h) (Э + х)

1-2/г

(2.65)

Задаваясь типом подшипника, характеристиками ротора, его дисбалансом, можно, пользуясь вхражением (2.65), найти необходимые усилия предварительного осевого натяга, при которых будет обеспечен минимальный уровень вибрации основной частоты. Но в то же время анализ показывает, что даже относительно малые изменения в осевом поджатии могут привести к значительным изменениям в общем уровне вибраций машины, что подтверждается часто на практике.

4. Субгармонические колебания ротора в подшипниках качения

Колебательные явления, возникающие при вращении вала в подшипниках качения, не сводятся только к колебаниям

основной частоты , частоты вращения вала. При вращении вала

в подшипниках качения возникают субгармонические колебания,

параметрические, комбинационного типа, зависящ.ие от большого числа факторов - скорости, нагрузки, геометрии дорожек и тел качения, чистоты контактируюш,их поверхностей, радиального зазора и нелинейности радиальной и осевой жесткостей подшипника. Все это вызывает значительные трудности в точном математическом описании движения ротора, приводит к необходимости упрощать задачи. В результате мы имеем лишь приближенные решения, правда удовлетворяющие в той или иной мере требованиям, предъявляемым практической стороной дела.

Как было показано в п. 2, нелинейная жесткая характеристика шарикового радиального подшипника, описываемая законом Герца, может быть представлена в виде аппроксимирующей функции f (у) ау -\- Ьуу и уравнение движения ротора по одной из координат записывается в виде

у + ау + Ьу = Ясо cos со/.

(2.66)

Уравнение (2.66) агносится х классу уравнений Дуффинга. Теоретически и экспериментально доказано, что в нелинейных системах, подчиняющихся уравнениям Дуффинга, существуют колебания, частота которых меньше частоты возмущающей силы в два или три раза. Такие колебания называются субгармоническими порядка 1/2 и 1/3 (в отличие от ультрагармонических, частота которых выше частоты возмущающей силы). Субгармонические колебания появляются в нелинейной системе в виде субгармонического резонанса, когда частота возмущающей силы кратна собственной частоте линейной системы [751. Уравнения, описывающие движение ротора в подшипниках качения, существенно нелинейны, а податливость самих шарикоподшипников приводит к значительному снижению резонансных скоростей, поэтому и субгармонические колебания валов на шарикоподшипниках могут возникать в рабочем диапазоне скоростей. /Гак как в уравнении (2.66) коэффициент при нелинейном члене того же порядка величины, что и при линейном, то для решения этого уравнения обычные асимптотические методы, используемые при исследовании квазилинейных систем, здесь не применимы. Воспользуемся методом изображающей функции, изложенным в монографии О. Блакьера [17]. Этот метод относится к частотным методам анализа и распространяет на нелинейные системы понятие передаточной функции, называемой в этом случае изображающей функцией.

Субгармонические колебания ротора в жестких подшипниках.

Предположим наличие в исследуемой системе вязкого линейного трения. Уравнение (2.66) после введения демпфирования примет вид

у +У]У + ciy + Ьу = Ясо cos со/.

(2.67)

Будем полагать, что в системе, описываемой уравнением (2.67), существуют субгармонические колебания порядка 1/2. В этом случае решение уравнения (2.67) будем искать в виде

у = Acqs (со/- г) + ficos / - . (2.68)

Подставим (2.68) в левую часть уравнения (2.67) и, обращаясь к методу изображающей функции, запишем:

= У + ЦУ + У--Ьу

Adi cos {(at - El)--7- X

Xcos-- - - т]Лсй81п ((at-Si) - T] (flsin {t - -\ + a A cos {Ы - El) H-aS cos (-- - 82) + Ь - Б (2 Л + + В") cos (1- - ea) + b IЛ (Л + 2B) cos \<л1 - +

+ ЬI Лб cos ("I (й - 2ei + Ёг) 4- 6 cos (- Ы - Зг"

bAB cos (282 -si)

(2.69)

Согласно определению изображающей функции допустимо применение комплексной записи для г/ (О и [/ (t):

у (t) = г/, (t) + (О = Л ехр [i {(at - г)] + В ехр[ i (-- ~ 82) ; (2.70)

и (О = у + цу + ау + Ь В (2Л + В) ехр (- f82)

ехр I I

(О л

А (Л 4- 2В) ехр (- J8i) ехр [Ш)

/о D3 1 / 3 \

b. ~ АВ ехр [- i(28i - 4)1 + -Р (- Зг)j ехр \i2t)

b ЛВехр [ t(ei -262)]

(2.71)

Перегруппировав одночастотные слагаемые, можно выражение (2.71) разделить на три части:

(/() = [/,(/) + [/,(/) +Д (/)= + т]1 + ar/i + Ь Г- (А +

Ух -h Уг Н- ЧУг Н- аУг

i ( оо/ - 28i

(2Л + В)

i - 4е.

АВ ехр {i{г - 6i)]iBexp (Щ,

(2.72) 93