наблюдались и при моделировании системы с предварительным осевым натягом, причем зона существования субгармоник располагалась за второй критической скоростью как в случае преднатяга, так и в случае зазора (моделировался ротор с двумя упругими опорами). ОбТасть существования субгармонических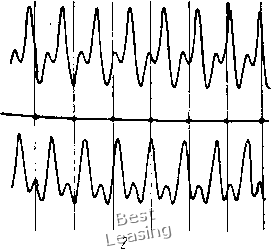

Рис. 2.26. Субгармонические колебания порядка 1/2 ротора в двух упругих шарикоподшипниках (решение на аналоговой вычислительной машине): а - неустановившийся режим колебаний; б -

установившийся режим;

/ - траектория движения шипа; 2 - осциллограмма колебаний tio двум координатам; 3 - фазовая траектория движения шипа

колебаний распространялась до (о = l,8coi, где

первая

критическая скорость ротора. Можно выделить два типа этих колебаний - установившиеся и неустановившиеся. Пример неустановившихся колебаний дан на рис. 2.26, а для со = l,65(Oi. На этом рисунке представлены: траектория движения шипа ротора, полученная на плоскости координат у я осциллограмма колебаний того же шипа по двум координатным осям у я z, фазовая

траектория движения этого же шипа в координатах i/ и у, снятые с экрана осциллографа при решении на аналоговой машине. На рис. 2.26, б даны те же характеристики на установившемся режиме колебаний при со l,69wi. Отличие установившегося режима колебаний от неустановившегося заключается в том, что

на неустановившемся режиме в решении присутствует некоторая переменная составляющая с малой частотой изменения. Решение показало, что частота прецессионного движения ротора равна 3/2(0. Следовательно, центр шипа описывает траекторию, подобную представленным на рисунке, за два оборота ротора. Здесь следует обратиться к выражению (2,82), дающему соотношение между амплитудой колебаний основной частоты и амплитудой субгармоники как функцию косинуса с частотой 3/2(о: теоретическая частота изменения радиуса прецессии и полученная в результате решения на АВМ совпадают.

Фазовый портрет системы аналогичен фазовому портрету, полученному аналитически Т. Хаяси [106], для системы, описываемой уравнением Дуффинга, как на установившемся, так и на* неустановившемся режимах. Т. Хаяси в своей работе отмечает, что подобная фазовая траектория проходится системой за удвоенный период возмущающей силы, т. е. за два оборота ротора в нашем случае.

При опоре вращающегося вала на подшипники качения кроме субгармонических могут возникать и так называемые комбинационные колебания [114], природа которых также связана с нелинейной жесткостью подшипника. Комбинационные колебания состоят из двух движений с частотами, соответствующими собственным частотам системы coi я« и (о Рг» причем абсолютная величина суммы или разности этих частот равна частоте вращения вала (О, которая является также и частотой возмущающей силы, обусловленной статической и динамической неуравновешенностями ротора. Максимумы амплитуд этих колебаний возникают при угловой скорости ротора-(О (0i coal-

Колебания ротора при этом представляют собой сумму "или разность двух движений с частотами pi я р- Если оба движения, имеющие место при комбинационных колебаниях, представляют собой прямую прецессию или оба обратную, то возникают только колебания суммарного типа.

В системах с упругими подшипниками качения отстройка от субгармонических и комбинационных колебаний состоит в перераспределении зон возможного возникновения указанных режимов колебаний относительно рабочей частоты вращения путем изменения жесткости упругого поля подшипника.

ГЛАВА 3 СНИЖЕНИЕ

ВИБРОАКТИВНОСТИ РОТОРОВ МАШИН

1. Повышение точнооти изготовления, балансировки и монтажа роторов

В предыдущих главах было установлено, что динамические нагрузки (вибронагрузки) на опоры роторых машин вызываются следующими факторами, или источниками виброактивности:

1) остаточной неуравновешенностью ротора после балансировки;

2) неуравновешенностью ротора в результате разбалансировки в процессе эксплуатации;

3) температурным эксцентриситетом ротора;

4) погнутостью вала;

5) радиальной несоосностью валов;

6) угловой несоосностью валов;

7) анизотропией жесткости ротора;

8) овальностью цапф в подшипниках скольжения;

9) дефектами деталей подшипников качения;

10) неравномерностью воздушного зазора в электрических машинах;

И) факторами, вызывающими автоколебания роторов (силы внутреннего трения в материале ротора и позиционные силы, действующие со стороны смазочного слоя на цапфу);

12) прочими факторами, носящими нерегулярный характер (задевание ротора о статор, дефекты приводных устройств и т. п.).

Уровень динамических нагрузок на опоры, вызванных отдельным фактором, зависит как от численной величины данного фактора, так и от упруго-инерционных и демпфирующих характеристик роторной системы. Последние определяют функциональную зависимость нагрузки от фактора.

Снижение уровня динамических нагрузок на опоры может осуществляться при этом как путем уменьшения численных величин перечисленных факторов за счет повышения точности изготовления, балансировки и монтажа роторов, так и путем направленного изменения функциональных зависимостей нагрузок от факторов за счет оптимального выбора упруго-инерционных и демпфирующих характеристик роторной системы.

В зависимости от. конструкции и условий эксплуатации роторной машины некоторые из перечисленных выше факторов могут заведомо отсутствовать. В целях конкретизации предположим,

что уровень нагрузок на опоры рассматриваемого типа роторных машин зависит от т факторов Qi (i = 1, 2, /п).

В реальных машинах любой фактор, за исключением анизотропии жесткости, является случайной величиной, которая может принимать значения в интервале от нуля до верхней границы поля допусков q*. Анизотропию жесткости ротора можно считать детерминированной величиной.

Векторы динамических нагрузок на опору R,-, вызванные факторами qi, являются вращающимися случайными векторами со случайными значениями начальных фаз. Скорость вра-

OA 0,2

0,5 10 15 2.0 2.5 х/бо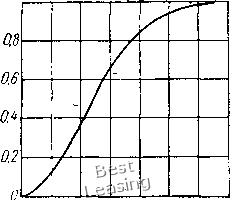

0.5; W 15 2.0 2.5 х/бо

Рис. 3.1. Плотность вероятности (а) и функция распределения (б) закона Релея

щения вектора R(- зависит от природы и может быть равна о) или кратна ей.

Известно, что погрешности геометрической формы деталей, ошибки взаимного расположения поверхностей и некоторые другие технологические неточности являются причинами факторов qi и подчиняются распределению Релея [23]. Кроме того, модуль случайного вектора, начальная фаза которого распределена равномерно, также подчиняется распределению Релея.

Распределение Релея определяется одним параметром Oq - радиальным средним квадратическим отклонением исходного двумерного нормального распределения, или круговым рассеиванием.

Плотность вероятности распределения Релея определяется по формуле .

fix)

О при л:<0.

при л: > О, .

(3.1)

где X-возможные значения случайной величины X, Функция распределения имеет вид

О при x<iQ,

-Fix)

При JO 0.

(3.2)

Графики плотности вероятности (3.1) и функции распределения (3.2) в зависимости от переменной xIoq показаны на рис. 3.1. Математическое ожидание и среднее квадратическое отклонение равны;

М [Х] - 1,253ао; а {ХУ= 0,б55ао. . (3.3)

Если известно предельное максимальное значение хах» которое может принимать случайная величина X, то числовые характеристики (3.3) легко могут быть определены с помощью правила «трех сигм». Согласно этому правилу, все практически возможные значения (точнее 98,89%), которые может принимать случайная величина X, находятся в пределах О л; Зод. Отсюда имеем ху За о, или

3 -тах*

Подставив (3.3) в (3.4), получим: М [X] 0,42;с; а [X]

0,22л;

max-

(3.4)

(3.5)

Аналогичным образом можно определить числовые характеристики случайных величин Ri. Задавшись для каждого фактора qt верхней границей поля допусков q* и вычислив соответствующие им максимальные динамические нагрузки R*, по аналогии с (3.5) можно записать:

М [Ri] 0,42i?;; о Ш 0,22i??. (3.6)

Суммирование вращающихся случайных векторов одной частоты целесообразно производить в системе координат, вращающейся с этой же частотой, так что векторы по отношению к ней будут неподвижны.

Для суммы статистически независимых векториальных случайных величин (случайных векторов с нулевым математическим ожиданием) справедливо следующее равенство [1]:

(3.7)

где 0-среднее квадратическое отклонение модуля суммарного случайного вектора; - то же i-ro случайного вектора. Тогда, из формул (3.6) и (3.7) получим:

М IR] 0A2R*ck; о [R] 0,227?*к. (3.8)

где R - модуль суммарного случайного вектора; Rl - среднее квадратическое значение модулей максимальных динамических нагрузок R*y определяемое выражением

(3.9)

Плотность вероятности и функция распределения модуля R описываются формулами (3.1) и (3.2) с параметром

ao4-i?c*K. (ЗЛО)

Теперь рассмотрим случай суммирования вектора V, имеющего постоянный модуль V и равновероятное распределение начальной фазы, с вектором W, имеющим распределение Релея. Предполагается, что вектор V вызван детерминированным фактором, например анизотропией жесткости ротора. Требуется найти закон распределения и числовые характеристики вектора Z - V + W.

проекции вектора V на декартовы оси координат ху подчиняются распределению арксинуса [1]. Плотность вероятности равна

О при Vjc - V\ при -V<Vx<V; (3.11)

a(Vx)

при у.

Математическое ожидание М [V,] = 0; среднее квадратическое отклонение о [V\ 0,7071/.

Проекции вектора W имеют нормальный закон распределения с плотностью вероятности

Ф (х) = -г=- хр (- wll2ol)y

(3.12)

где -круговое рассеивание модуля W.

Числовые характеристики: М IW] 0\ а = а.

Композиция законов распределения (3.11) и (3.12) имеет весьма сложный вид, поэтому ограничимся приближенным суммированием. При этом закон распределения величины = V+x аппроксимируем нормальным распределением, имеющим следующие числовые характеристики:

М [ZJ = М IVx] + М [Wx] = 0;

[VJ + [Wx] = 0,5V + а

Плотность вероятности

ехр [-21/2(0,51/ + 0)]. (3.13)

1/2я]/0,5К2+а;

Аналогичное выражение можно записать и для f (Zy). Исходному двухмерному нормальному распределению соответствует распределение модуля Z по закону Релея с круговым рассеиванием

(ЗЛ4)

00 = 1/" (у1 + 0,5У\