Однако второе явление, обнаруженное экспериментально Ла-валем и представляющее большой практический интерес,- легкий переход через критические скорости при сравнительно небольших резонансных амплитудах - не нашло объяснения в упомянутых работах Феппля и Николаи. Так как в этих работах сопротивлением пренебрегали, то при критических частотах вращения амплитуды теоретически неограниченно возрастали и указанное явление не могло быть объяснено. Следует отметить, что при

проведении эксперимен-

2,0 р/к

Рис. 3.8. Амплитудно-частотная характеристика вынужденных колебаний материальной точки. Уровень резонансных амплитуд зависит от отношения nIk

ления; k - собственная частота; h

та Лаваль никакого искусственного демпфирования не вводил, он только уменьшал толщину вала, снижая тем самым жесткость системы, и достиг удовлетворительных для практики результатов.

Между тем для объяснения этого явления достаточно рассмотреть амплитудно - частотную характеристику вынужденных колебаний материальной точки, дифференциальное уравнение которых имеет вид

X 4-2 пх 4- kx ~

h sin (pt 4- 6)*

где п - приведенный коэффициент сопротив-приведенная амплитуда

возмущающей силы; р - частота возмущающей силы

Амплитудно-частотная характеристика вынужденных колебаний представлена на рис. 3.8, где по оси абсцисс отложен коэффициент расстройки p/ky а по оси ординат - коэффициент динамичности A/Aq (А - амплитуда вынужденных колебаний; Aq = - - отклонение точки от положения равновесия под действием постоянной силы, равной максимальному значению возмущающей силы).

На рис. 3.8 [67] показано. Что с увеличением приведенного коэффициента сопротивления п амплитуда колебаний при резонансе значительно уменьшается. При увеличении от п = Oylk до = 0,25 амплитуда при разгоне уменьшается в 2,5 раза. Дальнейшее развитие инженерной мысли пошло по этому пути. Для уменьшения амплитуд колебаний стремились увеличить

коэффициент сопротивления. Широкое распространение .получило демпфирование колебаний путем введения в систему вал-опоры искусственных демпферов [95]. При этом не учитывалось отрицательное влияние увеличения демпфирования /г, в особенности отрицательное воздействие нелинейных искусственных демпферов.

1. Увеличение линейного сопротивления уменьшает амплитуду колебаний только в зоне резонанса, т. е. в зоне критических скоростей вращения, не оказывая какого-либо существенного влияния на уровень вибрации на рабочих режимах;

2. Увеличение линейного сопротивления приводит к уменьшению к. п. д., так, для простейшего случая вынужденных колебаний материальной точки, вызванных синусоидальной возмущающей силой, средняя отдаваемая мощность определяется по формуле [68]

= прЫт, (3.38)

где п - приведенный коэффициент сопротивления; р - частота возмущающей силы; А - амплитуда вынужденных колебаний; т - колеблющаяся масса.

Таким образом, на рабочих режимах с увеличением коэффициента сопротивления отдаваемая мощность растет пропорционально, тогда как амплитуда вынужденных колебаний вдали от резонанса остается практически неизменной, она почти не зависит от коэффициента сопротивления.

3. Нелинейные искусственные демпферы, которые конструировались с целью резкого увеличения коэффициента сопротивления, являлись причиной возникновения новых зон повышенной вибрации и, в частности, причиной возбуждения стойких автоколебаний.

Вернемся к амплитудно-частотной характеристике, представленной на рис. 3.8. Каждая кривая соответствует определенному значению п, выраженному в долях k - собственной частоты системы. Следовательно, каждая кривая соответствует определенному отношению (правая часть рисунка)

n/k = const. (3.39)

Следовательно, для увеличения этой постоянной и уменьшения амплитуды при резонансе имеются два пути: увеличение коэффициента сопротивления и уменьшение собственной частоты системы. Первый путь и его недостатки были обсуждены выше, второй путь был впервые использован Лавалем. Уменьшая диаметр вала, Лаваль уменьшал его жесткость и, следовательно, собственную частоту. Однако он не получил широкого распространения по ряду причин.

1. Созданию достаточно тонких валов часто препятствовали несовместимость с условиями прочности и невозможность обеспе-

чить конструктивные и технологические требования к роторным машинам. Так, например, современный компрессор высокооборотного газотурбинного двигателя по конструкции и прочностным требованиям не может быть выполнен в виде гибкого вала.

2. При вращении гибкого тонкого вала в зоне, расположенной выше критической скорости, внутреннее трение в материале вала, возникающее при изгибных колебаниях вала, превращается в отрицательное трение, раскачивающее вал.

3. При вращении гибкого вала, установленного в подшипниках скольжения, на скоростях, превышающих первую критическую скорость в два раза и более, возникают стойкие автоколебания большой амплитуды, препятствующие нормальной эксплуатации роторных машин.

В начале 50-х годов [53, 42] был теоретически развит и практически применен другой путь конструирования высокооборотных роторов. Не накладывая никаких ограничений на конструкцию и размеры ротора, сохраняя без изменения все его параметры, выбранные из оптимальных. условий эксплуатации, технологии изготовления прочности, легкий переход через критические скорости достигался установкой ротора в упругие, податливые опоры. Жесткость системы в связи с этим уменьшалась, отношение nik, определяющее уровень резонансных амплитуд, резко увеличивалось за счет уменьшения собственной частоты k, и переход через зоны критических скоростей происходил при весьма малых амплитудах.

Сопротивление движению при этом было минимальным. Его можно назвать естественным, так как никаких искусственных мер для его увеличения не принималось.

Динамика вала, вращающегося в упругих опорах, рассматривалась и ранее. Однако в этих исследованиях основное внимание было обращено на вычисление критических скоростей системы. Было установлено, что применение упругих опор снижает критические скорости.

Влияние податливости опор на уровень резонансных амплитуд и, следовательно, на переход через зоны критических скоростей, влияние упругих опор на давления между валом и подшипниками до этого не рассматривались. Между тем именно эти свойства роторной системы и представляют наибольший практический интерес, так же как и явление самоцентрирования.

Рассмотрим два способа применения упругих опор: а) вал, вращающийся в шарнирной и упругой опорах; б) вал, вращающийся в двух упругих опорах.

Динамика жесткого вала, вращающегося в одной шарнирной и второй упругой опорах. Рассмотрим горизонтальный вал, вращающийся с постоянной угловой скоростью вокруг оси симметрии (рис. 3.9). Левая опора - шарнирно-закрепленный самоуста-навлцвающийся подшипник, который может свободно поворачиваться вокруг центра 0. Правая опора - цилиндрический под-

шипник, упруго закрепленный в корпусе. Центр тяжести вала- точка С.

Проекции кинетического момента вала на неподвижные декартовы оси координат, проходящие через центр инерции вала, вычисленные с точностью до величин первого порядка малости включительно, равны [10]:

К = Л(о; Ку - Лор - 5у; = Ащ + Вр, (3.40)

где Л, В - главные центральные моменты инерции вала относительно оси симметрии и относительно оси, перпендикулярной оси симметрии; малые углы Р, у даны на рис. 3.10.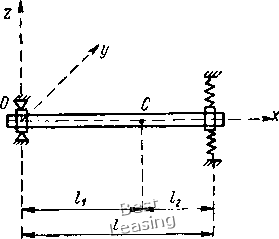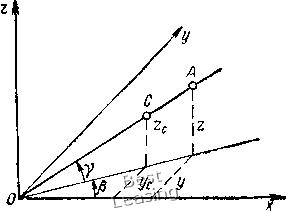

Рис. 3.9. Схема жесткого вала, вращающегося в шарнирной и упругой опорах

Рис. 3.10. Параметры, определяющие положения вала при колеба-. ниях

Обозначая координаты правой опоры г/, 2, запишем с точностью до малых величин первого порядка малости:

р у/1- у = z/l. (3.41)

Координаты центра тяжести вала:

Ус - yUl\ Z, = zyL " (3.42)

Пользуясь теоремой об изменении кинетического момента в проекциях на неподвижные декартовы оси координат, получим дифференциальные уравнения свободных малых колебаний [10] относительно осей, проходящих через левую шарнирную опору,

(В + МЛ) 2 - А(ду+ ctz 0; {В + МП) у + Ло)2 + cly = О,

(3.43>

где М - масса вала; с - коэффициент жесткости упругого поля

правой опоры; кососимметричные члены -Ащ и +Ло)2 учитывают действие гироскопических сил. Чем больше произведение Л (О, тем сильнее влияние этих сил.

При расчете роторных машин существенное значение имеют вынужденные колебания вала, вызванные статической и динамической неуравновешенностями.

Статическая неуравновешенность, вызванная неточностью изготовления и балансировки вала, задана смещением центра тяжести на малое расстояние е-эксцентриситета от геометрической оси вращения.

Динамическая неуравновешенность, возникающая по тем же причинам, определяется малым углом б между главной центральной осью инерции и геометрической осью вращения.

Тогда, при смещении упругой опоры координаты центра инерции определяются формулами, отличными от (3.42),

е cos 0)/; г. = 2

е sin со/.

(3.44)

Углы, образованные главной центральной осью инерции с координатными плоскостями xz и ху, с учетом (3.41) определяются по формулам:

Pi = Р + 6 cos {Ы - г) Ti = Т + б sin (ю/ - е)

б cos (о)/-е); б sin - е).

(3,45)

В этих формулах р, 7 - углы, образованные геометрической осью вращения с плоскостями xz и ху, а угол Ы-г образован плоскостью, проходящей через ось вращения и главную центральную ось инерции, с плоскостью ху. Проекции кинетического момента на оси координат равны:

Ксу = Ло)р1 - Б71; Ксг = Ащх + 5Pi. (3.46)

Воспользовавшись теоремами о движении центра инерции и об изменении кинетического момента, составим дифференциальные уравнения малых колебаний вала:

-су -cz

Rlz\

A o)pi

Ло)71

~ B71 = ca/g + R-Lzl-Ly fipi -cyl<2, - Riylx,

(3.47)

где Ус, Zc - координаты центра инерции вала; Ry, R - проекции реакции шарнирной опоры. В эти уравнения входят проекции реакции шарнирной опоры. Исключив эти проекции из системы четырех дифференциальных уравнений, получим окончательно:

М1\) Z - Ащ + cfz = Mevihl sin (at + (5 - Л) ЫЬ sin (со/ - 8);

{В + МЩ у

(3.48)

Лсог + сРу = Me(x>hl cos (x>t

(В - А) /0)26С05 (О)/ - 8).

Полное решение данной системы обыкновенных неоднородных линейных дифференциальных уравнений с постоянными коэффициентами складывается из общего решения однородной системы

II частного решения неоднородной системы. Сопротивление, которое в уравнениях (3.48) не учитывалось, приводит к быстрому :штуханию членов, соответствующих общему решению однородной системы, поэтому свободные колебания, определяемые общим решением однородной системы, могут иметь существенное значение только при изучении переходных режимов: пуск, остановка машины и переход от одного режима к другому.

Вынужденные колебания вала определяются частным решением системы (3.48). Это частное решение имеет вид:

г cos (o)f - а); z = г sin (со/ - а).

(3.49)

arctg

«1

«1

MeisHil +(B - A) ЫЧ cos e ,

c/2 - (5 + Mil - A) 0)2

(B - A) /0)26 sin e ci-.(BJMll - A) 0)2

(3.50)

Таким образом, при вынужденных колебаниях вала его ось описывает круговой конус с вершиной в точке О, вращаясь с угловой скоростью 0) в направлении собственного вращения вала. Это движение называется прямой синхронной прецессией.

В инженерной практике наиболее существенное значение имеют амплитуда вынужденных колебаний и давление между валом и опорами. Для подавляющего большинства роторных машин модуль амплитуды колебаний регламентирован ГОСТом или другими техническими условиями. Давления между валом и опорами определяют в основном ресурс подшипников.

Если приравнять нулю определитель системы алгебраических уравнений, полученных в результате подстановки частного решения в дифференциальные уравнения (3.48), то найдутся критические скорости вала:

eol=====-; 0)2 = Tr======f . (3.51)

Vb + mi\ - a

Vb-miia

Однако, как следует из (3.50), при вынужденных колебаниях вала, вызванных статической и динамической неуравновешенно-стями, существует только одна критическая скорость o)i. Чтобы в этом убедиться, достаточно приравнять в (3.50) знаменатель нулр.

Как показано в работе [10], обе критические скорости существуют при действии на вал синусоидальной возмущающей силы постоянного направления, однако в инженерной практике этот случай маловероятен.

Амплитудно-частотные характеристики жесткого вала при вынужденных колебаниях, вызванных неуравновешенностью,