На рис. 1.6 показан характер зависимостей и « от угловой

скорости (0.

Внешнее демпфирование в рассматриваемой системе снижает амплитуды вынужденных колебаний L и w, а также несколько сужает интервал неустойчивости, который, как было показано выше, без учета демпфирования имеет границы coi и сод.

Динамические нагрузки на опоры. Вычисление динамических нагрузок на опоры, вызванных фактором двоякой жесткости вала, произведем в предположении, что зона рабочих скоростей

ротора не содержит интервала неустойчивости. В этом случае наибольший интерес представляют колебания под действием силы тяжести диска, поскольку колебания под действием неуравновешенности принципиально не отличаются от случая системы с круглым валом. Иными словами, двоякую жесткость вала и неуравновешенность массы диска можно рассматривать как два независимых друг от друга фактора.

Для случая абсолютно жестких опор проекции вектора динамической нагрузки, вызванной силой тяжести диска, на подвижные оси координат I и ц составляют:

= 0,5cil == 0,5cia cos = О.Бсу] = ОЬсЬ sin со.

Введем комплексную величину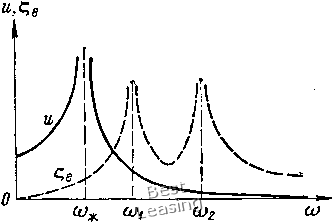

Рис, 1.6. графики амплитуд вынужденных колебаний центра вала двоякой л<есткости:

---~ под действием эксцеитрнситета центра тяжести диска;--под действием

веса диска

R = Rl + iRj = и ехр Ш + V ехр {-iwt)y

(1.28)

и = 0,25 (са + сЬ); V - 0,25 (са - сф). (1.29)

В неподвижной системе координат выражение (1.28) имеет

R = и ехр 2Ш + V, f/TOs 2Ы -\- V\ Ry и sin 2(0

Таким образом, нагрузка на опору складывается из вектора динамической нагрузки, вращаюш,егося с частотой 2ш w имего-ш,его модуль (/, и вектора дополнительной статической нагрузки, действуюш,его в вертикальном направлении и имеющего величину V.

Введем следующие безразмерные величины: 3 ш/соз - относительная скорость вращения вала; а = = {02 - Ci)l{c2 + Ci) = (coi - (of)/(coi + coi) - парамстр, характе-

ризующий анизотропию жесткости вала; /? = 2U/{mg) - динамическая нагрузка на опору, отнесенная к статической. нагрузке.

Тогда для величины /? с учетом (1.22), (1.29) и введенных обозначений .имеем следующее выражение:

(1.30)

В реальных конструк- fy

циях, как правило, а <С 1- и В этом случае формула (1.30) принимает вид

1 - 4Р=

а. (1.31)

Зависимость R4a = f (Р) графически изображена на рис. 1.7. Из формулы (1.30) / следует, что /? -> оо, если со -> со. При малых а величина (0 0,5(02. С увеличе- нием со величина 7?стремится не к нулю, как, например, амплитуда колебаний центра вала и (рис. 1.6), а к асимптоте

0,5 1,0 1,5 2,0 fi-(o/(Oz

(1.32)

Рис. 1.7. Динамические нагрузки на опоры ротора двоякой жесткости под действием собственного веса:

--- - - абсолютно жесткие шарнирные опоры; -~--с учетом масляной пленки подшипников скольжения

Формула (1.32) может быть использована для приближенной оценки уровня нагрузок на опоры, а именно: на закритических скоростях вращения (со > соз) динамическая нагрузка на опору, отнесенная к статической примерно равна параметру а, характеризующему анизотропию жесткости вала.

В предыдущих исследованиях не учитывались силы внешнего сопротивления, которые всегда имеют место в реальных роторных машинах. Их влияние рассмотрим на примере масляной пленки подшипников скольжения, которая, как известно, обладает достаточно хорошими демпфирующими свойствами.

Предположим, что опорами рассматриваемого выше ротора служат подшипники скольжения, масляная пленка которых имеет изотропную жесткость и демпфирование с коэффициентами Со и Kq соответственно.

Для вывода уравнений движения совместим начало систем координат ху и 1г\ с соответствующей для данной угловой скорости точкой кривой подвижного равновесия центра цапфы в подшипнике скольжения.

Через X, Уу , т] обозначим координаты центра тяжести диска; через Xq, у, Ло-координаты центра цапфы.

2 А. с. Кельзон и др.. .17

Тогда со стороны масляной пленки на безмассовую цапфу будут действовать две силы: сила упругости масляной пленки с проекциями на подвижные оси координат -Соо; -оПо сила сопро-

тивления с проекциями -Хо(1о-По); ->о(По + о)*

Со стороны вала на цапфу действует одна сила, имеющая проекции 0,51 (g- о); 0,52(11 - т]о).

С учетом изложенного дифференциальные уравнения движения системы при ех = = О будут иметь следующий вид:

т {I т (г)

2соЕ

По)

2соТ1о

(5о"

rio) + 2хо(г1о + со go)

= mg cos (0; -mg sin со/, (orio) = 0; : 0.

(1.33)

Введением безразмерных величин

= lib; ri = ri/б; S; = IJb; = ц,1Ь; a (c

у 2co/(m(o) 2cq/c2; v = 2xo/(m(02); F = /(бсо!);

3 = (o/cog; T 0)2; q = (l - ot)/(l + a),

где б - радиальный зазор подшипника, уравнения (1.33) приводятся к безразмерному виду:

Р)Г1

2рг1 2BS

По =

F cos рт; -F sin Вт;

9) 5о (I

vptio Y) Ло

0; 0.

(1.34)

В уравнениях (1.34) и в дальнейшем точки обозначают дифференцирование по безразмерному времени т, штрихи для простоты записи опущены.

Частное решение системы неоднородных уравнений (1.34) отыскивается в виде:

I = ах cos рт + Ьх sin рт;

So По

а 2 cos рт

2 sin рт; аз cos рт Ц- Ьз sin Рт; ал cos Вт + Ьл sin Вт.

(1.35)

Подставив (1.35) в (1.34) и приравняв соответствующие коэффициенты при одинаковых тригонометрических функциях в левой и правой частях уравнений, получим систему из восьми алгебраических уравнений относительно Uj и bj (/ = 1, 2, 3, 4), которая из-за громоздкости здесь не приводится.

Пользуясь комплексным представлением векторов, можно записать:

S = + Щ = и ехр фт + v ехр (-фт); ir\q = Uq ехр /рт + Vq ехр (-/рт),-

(1.36)

где Uj v\Uq, Vq-комплексные числа вида:

Ux 2

0,5 (ах

0,5 {а 2

ttl 2i 0

0,5 (аз - bx)\ Vx

Шо2» Vq2\

= 0,5 (ax

62); «2

bi); «01 0,5 (аз + 4); «02 = 0,5 (a -- 0,5 (из - 4); 0 2 - 0,5 (a4 + Ьз).

(1.37)

в неподвижной системе координат векторы перемещений имеют вид:

2 = 2 ехр /рт = и ехр 2фт + о;

2о = So Хр фт == «о 2/Рт + Vq, j

(1.38)

Таким образом, векторы перемещений центров диска и цапфы имеют динамические составляющие удвоенной частоты с комплексными амплитудами и и Uq, и статические составляющие v и Vq.

Комплексная динамическая составляющая реакции масляного слоя равна

(Cq 2шщ) б«о ехр 2i(x)t,

(1.39)

где = б«о хр 2i(i)t - динамическая составляющая перемещения центра цапфы.

Введением безразмерной величины

- 2R/{mg)

выражение (1.39), с учетом прежних обозначений и упрощений в записи, приводится к безразмерному виду

(7 2фv) ехр 2фт.

(1.40)

Модуль вектора динамической нагрузки на подшипник скольжения

V{ulx + uh) (7 + 4pV),

(1.41)

где величины Uqx й Uq определяются по формулам (1.37).

В соответствии с приведенными выше формулами были произведены расчеты динамических нагрузок на опору в широких диа- пазонах изменения параметров а, f и р. При расчетах использовался подшипник с дугой охвата .180° и IID = 1, динамические

2* 19

характеристики масляного слоя которого определялись по формулам:

J 2»

3 Z

(1.42)

где fi - динамическая вязкость масла; = 28/D - относительный радиальный зазор; /, D - длина и диаметр цапфы; /i, J2 - безразмерные коэффициенты, выражаемые через коэффициенты Л--8 работы [95] по формулам:

/i-= 0,5 (Л+ /4);/2-0,5 (/5+ /8).

Значения коэффициентов /j, /4, /5, /д в зависимости от коэффициента нагруженности подшипника , определяемого по формуле

- (mgyh)/{2tDiiw),

приведены в приложении 3.

Безразмерные коэффициенты у и v с учетом формулы (1.42) имеют вид:

Л; V

* 2>

где - коэффициент нагруженности при со

Анализ результатов расчетов показывает, что влияние масляной пленки сказывается в значительном снижении амплитуды колебаний и динамических нагрузок лишь при частотах вращения, равных или близких к критической частоте второго рода со, которая для малых значений параметра ос примерноравна 0,5оо2. На всех других частотах вращения заметного влияния масляной пленки на колебательный процесс не обнаружилось.

С увеличением нагруженности подшипниковили с уменьшением параметра F относительные динамические нагрузки на опоры несколько уменьшаются. Однако для достаточно широкого класса роторов двоякой жесткости, опирающихся на подшипники скольжения и имеющих а < 0,1, динамические нагрузки на опоры могут быть определены с помощью графической зависимости, представленной на рис.Ч.7.

Пример 1,1. требуется определить уровень динамических нагрузок на опоры ротора турбогенератора, вызванных фактором двоякой жесткости. Расчетная схема ротора приведена на рис. 1.8.

Известно, что рабочая частота вращения ротора равна 50 Гц, а его критическая частота, измеренная экспериментально, составляет 63 Гц. Основные размеры ротора: /1 = /а = 3 = 90 см; = dg 22 см; = 52 см; Di = 28 см. Бочка ротора имеет 16 продольных пазов.

Произведем расчет анизотропии жесткости ротора,

Главные моменты инерции площади сечения бочки ротора с учетом симметрии сечения относительно координатных осей и -г) определяются выражениями:

~ 64

16 16

"бГ "бГ

4 S hk; ft=i

4 S 1ф

(1.43)

где Ik - моменты инерции площади паза с номером k относительно соответствующих осей.

5? fj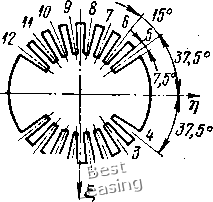

Рис. 1.8. Расчетная схема ротора генератора двоякой жесткости

С учетом формул = г cos ф, т = г sin ф, = г dr выражения для 1 и /feH меют следующий вид:

Hz f2k

Rt~Ri 1

Hi Ф

г sin 2 Ф ф =

Ik 1

(ф2й - ф1/г) - у (Sin 2ф2/г - Sin 2ф1)

i?2 2ft

2 dS = cos2 (pd(pdr =

Hi Ф

Ri-Rt 1

Ik 1

(1.44)

(ф2: -Ф1) +"2"(Sin 2ф2й-sin 2ф1й)

где Ri = Di/2; R2 = 02/; <pik и cp2k - угловые координаты сторон -го паза (рис. 1.9).

В соответствии с выражениями (1.43) и (1.44) находим:

0,153 (Ri - R\) - 29,5.10 см4;

= - 0.370 (Rl - R\) = 20,4-10* см

Пусть /j, J2 и /3 - моменты инерции площадей сечений участков ротора, имеющих длины Z, I2 и /д соответственно (см. рис. 1.8). Тогда жесткость посере-