расстоянию от центра инерции до шарнирной опоры, а составляющие силы равны эквивалентной силе инерции.

Кривые давлений для данного случая приведены на рис. 3.16, а, б в виде штриховых линий. Динамическая неуравновешенность резко увеличивает давления на шарнирную опору, в особенности при консольном расположении центра инерции.

Найдем предельные значения безразмерного давления на шарнирную опору RJiMeoy) при неограниченном возрастании частоты вращения вала.

У вала есть только статическая неурав-новешенность(& = 0)

С0->-оо

d + Ш1 1-d

(3,97)

У вала есть только динамическая неуравновешенность (е = 0),

Прилагая эквивалентную силу инерции в центре инерции вала, находим

W->-oo

1 + p/i 1-d

(3.98)

Ротор имеет статическую скую неуравновешенности

и динамиче-

±b/k + ld + p{l,/l±b/l)] 1 - d

(3.99)

В последней формуле надо брать знак плюс при удалении точки приложения эквивалентной силы инерции от центра инерции вала в направлении от шарнирной опоры и знак минус при ее приближении к шарнирной опоре. Рассмотрим вначале случай безмассовой упругой опоры р = 0.

Из выражений (3.62), (3.86), (3.97)-(3.99) и кривых на рис. 3.14-3.16, а, б можно оценить влияние статической и динамической неуравновешенностей на развитие вибраций вала и его давлений на опоры.

Вибрации вала и его давления на упругую опору пропорциональны величине hs в (3.62), (3.75), поэтому при равных величинах статической и эквивалентной динамической неуравновешенностей вибрации вала и его давления на упругую опору будут одинаковыми.

Иная картина наблюдается для давлений на шарнирную опору. Из (3,97) и (3.98) и рис. 3.16, а, б видно, что эквивалентная динамическая неуравновешенность, равная по величине статической, при d < 1 вызывает давления на шарнирную опору, во много раз превышающие давления от статической неуравновешенности. Поэтому можно утверждать, что если эквивалентная динамическая неуравновешенность будет соизмерима со статической, то 136

в зарезонансной зоне давления на шарнирную опору будут вызваны в основном действием динамической неуравновешенности. Между тем действие динамической неуравновешенности пропорционально разности между центральными экваториальным В и полярным А моментами инерции (3.59). Отсюда следует, что для снижения вибраций и давлений на обе опоры вала, и особенно на шарнирную, полезно при конструировании уменьшать разность В - А.

Из (3.97) и (3.98) следует, что при больших скоростях вращения вала влияние статической неуравновешенности на увеличение давлений на шарнирную опору пропорционально величине d, учитывающей действие гироскопических сил. Влияние динамической неуравновешенности на давления в шарнирной опоре при малых d практически не зависит от гироскопических сил при больших частотах вращения.

Из рис. 3.16, а, б, а также зависимости (3.99) видно, что при заданных статической и динамической, неуравновешенностях вала давления на наиболее нагруженную шарнирную опору уменьшаются при удалении центра инерции вала от шарнирной опоры (увеличение /j), а зона, в которой могут располагаться давления на эту опору, сужается.

Рассмотрим влияние приведенной массы невращающихся де-•талей, совершающих колебания вместе с упругой опорой, на изменение давления на шарнирную и упругую опоры. Из (3.97)-(3.99) видно, что увеличение р ml/B при наличии у вала любого типа неуравновешенностей будет увеличивать давление на шарнирную опору. Из (3.74) следует, что при малом вязком трении на данной частоте вращения давления на упругую опору можно сделать малыми, если подобрать параметры упругой опоры таким образом, чтобы 1 - Pv = 0. Однако этот путь снижения давлений на упругую опору применим для рассматриваемой схемы вала, вращающегося в шарнирной и упругой опорах, только в случае, если он не ведет к увеличению приведенной массы упругой опоры. В противном случае некоторые уменьшения давлений на сравнительно менее нагруженную опору будут сопровождаться возрастанием давления на шарнирную опору, которая обычно значительно сильнее нагружена, чем упругая.

Полученные формулы позволяют провести детальный анализ влияния приведенной массы упругой опоры на давления вала на шарнирную и упругую опоры для конкретной роторной машины и выбрать ее оптимальное значение.

Сопоставление предельных значений давлений на шарнирную опору (3.97)-(3,99) с представленными на рис. 3.16, а, б кривыми показывает, что уже при у 4 давления в масштабе Ме(о лишь на несколько процентов превышают их предельные значения при неограниченном возрастании частоты вращения вала. Следовательно, при проведении ориентировочных расчетов давлений на опоры вала при заданных статической и динамической неуравно-

вешенностях можно пользоваться выражениями (3.88), (3.97)- (3.99).

Сравнение кривых на рис. 3.15 и 3.16, а, б, пересчитанных к одному масштабу, показывает, что в зарезонансной области, где выгодно использовать вал с одной упругой опорой по сравнению с валом, имеюш,им две жесткие опоры, давления на шарнирную опору в несколько раз превышают давления на упругую опору, причем с возрастанием частоты вращения эта разница растет.

Кривые на рис. 3.14-3.16, а, б показывают также, что если рабочие скорости в три-четыре раза выше критической, то дальнейшее снижение жесткости упругой опоры не дает заметного снижения вибраций и давления на шарнирную опору.

Подведем итог теоретических исследований динамики вала с одной упругой опорой.

1. Для уменьшения вибраций вала и его давлений на опоры рабочие скорости при наличии одной упругой опоры надо располагать в зоне, превышающей более чем в три-четыре раза первую критическую скорость, но далекой от второй критической скорости, форма колебаний при которой связана с изгибом вала.

2. Уменьшение жесткости упругой опоры приводит к уменьшению давлений на эту опору при рабочих скоростях, расположенных вдали от резонансной зоны, и к снижению вибраций вале при прохождении зоны критической скорости.

3. При вращении в зарезонансной зоне из двух опор наиболее нагруженной оказывается шарнирная. Давление на эту опору возрастает пропорционально квадрату частоты вращения вала и почти не зависит от вязкого трения в демпфере и жесткости упругой опоры.

4. Давления на шарнирную опору уменьшаются при удалении центра инерции вала от шарнирной опоры.

5. Динамическая неуравновешенность в несколько раз интенсивнее, чем статическая, увеличивает давления на шарнирную опору. Поэтому для увеличения ресурса таких роторных машин должна особо тщательно выполняться динамическая балансировка.

6. Давления на упругую опору имеют инвариантную частоту вращения, при которой они не зависят от вязкого трения. Эта скорость в 12 раз выше первой критической.

7. Динамические давления на упругую опору до прохождения инвариантной угловой скорости уменьшаются, а после ее прохождения быстро возрастают с увеличением вязкого трения.

8. При отсутствии вязкого трения давления на упругую опору при удалении рабочих скоростей от первой критической скорости остаются постоянными. При наличии вязкого трения давления на упругую опору возрастают в этой зоне почти пропорционально возрастанию частоты вращения вала.

4. Динамика жесткого вала, вращающегося в двух упругих опорах. Самоцентрирование

Вал, вращающийся в шарнирной и упругой опорах, можно рассматривать как жесткий только при частоте вращения, меньшей второй критической скорости. Переход через вторую критическую скорость для такого вала затруднен. Такой вал, рассматриваемый как жесткое тело, не самоцентрируется. Существенно снизить давления можно только между валом и упругой опорой. Эти недостатки устраняются при установке вала в две упругие опоры.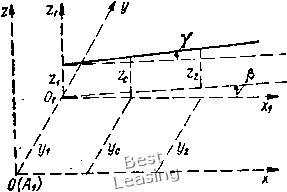

Рис. 3.17. Схема жесткого вала, вращающегося в двух упругих опорах

Рис. 3.18. Параметры, определяющие положение вала при колебаниях

Рассмотрим [42, 43 ] динамику горизонтального жесткого вала массой М, вращающегося в двух упругих опорах (рис. 3.17). Коэффициенты жесткости упругого поля левой опоры Ci, правой с. Центр инерции вала вместе с подшипниками находится в точке С, расположенной на расстоянии от левой и /g от правой опоры. Вал вращается с постоянной угловой скоростью оз. Главные центральные моменты инерции равны А относительно оси симметрии вала и В относительно оси, перпендикулярной к оси симметрии (при вычислении момента инерции В учитывается масса вала и подшипников, колеблющихся вместе с валом). Расстояние между опорами /. Вал не уравновешен.Статическая неуравновешенность задана эксцентриситетом е,.динамическая - углом б, образованным главной осью инерции и геометрической осью вращения. Плоскости, проведенные через геометрическую ось и центр тяжести, а также через геометрическую ось и главную ось инерции, образуют двугранный угол г. Для составления дифференциальных уравнений движения вала рассмотрим его смещенное положение (рис. 3.18). Тогда на основании теоремы о движении центра инерции и теоремы об изменении кинетического момента в относительном движении по отношению к центру инерции можно записать:

Ащх + Бр1 == с-хУх ~

-C-iZ

2-2»

- Cil\Zx\

(3.100)

Здесь Ус, z, - координаты центра инерции; у, и уу 2 - координаты левой и правой опор; 71 и р - малые углы между проекцией главной центральной оси инерции на плоскость xz и осью X и между проекцией главной центральной оси инерции на плоскость ху и осью х. Тогда, учитывая статическую и динамическую неуравновешенности, составим равенства:

- " " ecosco; Zc = Zi~

ч - ч

г sin Ы\

б cos (со - е); =

- б sin (со - е).

(3.101)

Подставив эти значения переменных в систему уравнений (3.100), получим окончательно:

• • • •

(*12 + ssf/i) + Oilyx + с4Уг == МеЫ cos (oif;

• • • •

(*i22 + гх) + + clz = МеЫ sin (oi; Ло) (i/2 - ;) - В (2*2 - 2i) - + Cxlfix =

\o. 1 \)Z )

(B -A) /(06 sin ((Of - 8);

Лео (22 - Zx) + B {У2 - У1) + chly + cJilyi = (B - A) /озб cos (o)f - e).

Эта система обыкновенных линейных неоднородных дифференциальных уравнений -с постоянными коэффициентами описывает малые колебания, вызванные статической и динамической неуравновешенностями. Решение этой системы складывается из обш,его решения однородной системы и частного решения полной системы. Общее решение однородной системы описывает свободные колебания ротора: При учете сил сопротивления эти члены быстро затухают, поэтому могут иметь значение только в переходных режимах, при пуске и останове машины, а также при переходе с одного режима на другой. Частное решение описывает вынужденные колебания. Эти колебания не затухают и при учете сил сопротивления. Вынужденные колебания представляют наибольший интерес с инженерной точки зрения, так как определяют ресурс роторной машины, уровень вибрации и давления между валом и опорами на рабочих режимах.

Частное решение полной системы имеет вид:

fli COS (A)t + sin co; Zi = sincof - bi cos (dt; аз cos (xit + Ьз sin (oi; Z2 = аз sin cof - 63 cos cof, J

(3.103)

, , , Mdco [(B - Л) co - cUJ] /2 (0))

(yW/i(o - cl) (B - A) /бсо cos e}; -4 Melby" l(B - Л) co - Ш] - (М/со - cJ) {В - Л) /бш cos 8

/2 («)

/2 И

(M/iO) - cl) [В - Л) /6(0 Sin е; (УИ/2Ш - Cxl) {В - А) l8of Sin 8

(3.104)

при условии, что

/2 (со) = ЦВ - А) «2 - chl] {Oil - М/зО)) -- [[В - Л) - Ci/Zi ] (Mlioy - С2О =f 0.

(3.105)

При /2 (to) = О наступает резонанс, амплитуды колебаний согласно (3.104) неограниченно возрастают, а корни этого уравне-. ния определяют критические скорости. Они равны

«1.2

Ni ± lNl - Ш (£1- Л) СуСГ 2М (В - А)

(3.106)

N\ = {ci + С2) {В-А) + М {cxll 4- ЫЬ-

При проектировании горизонтальных роторов полезно удовлетворять равенству

cjc = /sZ/i (3.107)

При этом условии ротор в положении статического равновесия горизонтален, а частотное уравнение принимает более простой вид

[{В - Л) (0 - cjji (Cil - М/2Со) (1 + /1 2) = 0. (3.108)

Корни этого уравнения, определяющие критические скорости, будут:

(ЗЛ09) (3.110)

0)1 - Vcilit/{B - Л);

0)2 =="KCi (M/2).

В зависимости от конкретных параметров ротора, одна из этих критических скоростей будет больше другой.

В случае, когда критическая скорость определяется равенством (3.109), резонансные амплитуды зависят только от динами-