дине ротора, вычисленная с помощью интеграла Максвелла-Мора для случая = /2 = /3 = /, выражается формулой

(1.45)

С ==

Значения максимального Cg и минимального коэффициентов жесткости ротора найдем, если в выражение (1.45) вместо /д подставим соответственно величины Il и При Е = 2-10 кгс/см2, / = 90 см, /i = /3 = И 500 см* находим: Са = 17,4 • 10* кгс/см, = 16,7 10 кгс/см.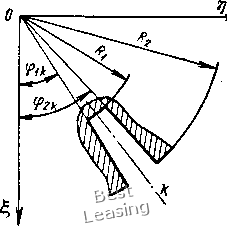

Рис. 1.9. К определению моментов инерции площади поперечного сечения -го паза

Рис. 1.10. Форма сечения вала, обеспечивающая выравнивание жесткости ротора

Параметр, характеризующий анизотропию жесткости ротора,

С2 - Ci

С2 +ci

0,021.

Учитывая, что р = ю/юд = 0,8, по формуле (1.31) или с помощью рис. 1.7 находим: R = 1,64а = 0,0345.

Таким образом, в данном примере двоякая жесткость ротора вызывает динамические нагрузки на опоры с частотой 100 Гц и с амплитудой, равной 3.45% от статической нагрузки на опору.

Рассмотрим задачу о выравнивании коэффициента жесткости ротора.

Очевидно, что если сечения участков вала, поддерживающих бочку ротора, будут иметь неравные главные моменты инерции площади, причем эллипсы инерции последних будут ориентированы малой полуосью по направлению большой полуоси эллипса инерции сечения бочки ротора и наоборот, то при определенных условиях может произойти выравнивание коэффициента жесткости ротора.

Пусть I = 1 = J\ I I, Тогда, как следует из выражения (1.45), выравнивание жесткости произойдет, если будет выполняться следующее равенство:

h 19 h~

8

(1.46)

Подставив в (1.46) найденные ранее значения / и получим

(т1 - h)KhAi = 3,6.10-6

(1.47)

предположим, что с целью выравнивания жесткости ротора, участки вала имеют постоянную по всей длине форму сечения, изображенную на рис. 1.10.

Соответствующие главные моменты инерции площади сечения вала определяются формулами [97]:

я -29

sin 46

= 4--у sin 0COS 0.

Построив зависимость (Jy - Jl)/(JlJt{) от 6, увидим, что условие (1.47) выполняется при 0 == 16°.

По формуле /г = cos 6 22 cos 16° = 21,2 см. Таким образом, для выравнивания жесткости ротора необходимо выполнить по всей длине участков вала двусторонние продольные срезы на глубину 0,4 см. Можно предположить, что такая глубина среза не окажет значительного влияния на прочностные свойства ротора.

3. Виброактивность подшипников скольжения вследствие некруглости цапф

При.расчетах динамических нагрузок в подшипниках скольжения роторных машин обычно принимается, что цапфа (шип) имеет правильную цилиндрическую форму. В действительности же реальная форма цапф имеет отклоне1Ия от цилиндрической как в продольном сечении - конусность, корсетность, так и в поперечном - некруглость.

Совершенно очевидно, что динамические возмущения в подшипнике скольжения могут вызывать лишь такие виды отклонений формы цапфы, которые приводят к изменению толщины масляного слоя в.процессе вращения цапфы с постоянной угловой скоростью. Из перечисленных видов к таким отклонениям относится только некруглость цапфы.

Отметим, что по этой же причине любые отклонения формы вкладыша подшипника от цилиндрической не могут быть причиной динамических возмущений.

Основными факторами, приводящими к некруглости цапф, являются: некруглость или изогнутость заготовок, изменение положения оси шпинделя в процессе обработки, нестабильные физико-химические свойства материала заготовок, односторонний износ в процессе эксплуатации и др. 1102].

Опыт эксплуатации роторных машин показывает, что некруглость цапф может быть причиной значительных вибраций подшипников скольжения. Так, например, при разности между наибольшим и наименьшим значениями диаметра цапфы 20 мкм и более роторы мощных паровых турбин подлежат выбраковке [93].

Рассмотрим влияние некруглости цапф на характер и величину динамических нагрузок в подшипниках скольжения.

Аналитические выражения профиля поперечного сечения цапфы. Предположим, что профиль поперечного сечения цапфы имеет произвольную форму (рис. 1.11). Для аналитического представления текущего размера профиля введем полярную систему координат, полюс которой совместим с центром тяжести площади поперечного сечения. Проведем в произвольном направлении полярную ось OiL. Тогда в данной системе координат положение

произвольной точки М контура поперечного сечения цапфы будет определяться полярным радиусом г и полярным углом ф.

Построим зависимость /- - /- (ф) и представим ее в виде конечного усечения ряда Фурье

Г(ф) =Го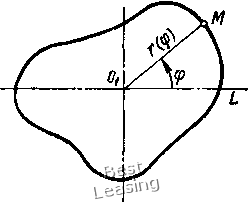

Рис. 1.11. Поперечное сечение некруглой цапфы

S (агСОЗЙф

+ Ь,зшФ), (1.48)

где т - наибольший порядковый номер гармоники. Гармоники порядка /п + 1 и более характеризуют .микрогеометрию (шероховатость) поверхности цапфы.

Коэффициенты разложения (1.48) определяются известными формулами:

г(ф) ф;

г (ф) COS ф йф; bk

г(ф) sin кц> йц>.

Выражение (1.48) можно также записать в виде

/(ф) = /0+ S /*й5Ш(ф

(1.49)

где Го - радиус средней окружности; rk = У~al + Ы плитуда k-й гармоники; = arctg -фаза fe-й гармоники.

Для фиксированного значения k из выражения (1.49) получаем уравнение контура поперечного сечения цапфы, имеющей элементарный вид некруглости,

й(ф)

sin (Аф + сс) ( = 2, 3, . . т). (1.50)

Так, при k = 2 слагаемое правой части (1.50) выражает овальность (рис. 1.12, а), при = 3- огранку с трехвершинным про-

филем (рис. 1.12, б), при k = i- огранку с четырехвершинным профилем (рис. 1.12, в) и т.д. 1102].

Отсутствие в выражениях (1.48)-(1.50) первой гармоники (k = 1) объясняется соответствующим выбором расположения полюса Oi полярной системы координат. Действительно, совмещение полюса Oi с центром тяжести площади сечения требует, чтобы для каждого элементарного вида некруглости /(ф) = Га + rsin (ф + (Xf) ( 1, 2, . . ., т) выполнялось условие отсут-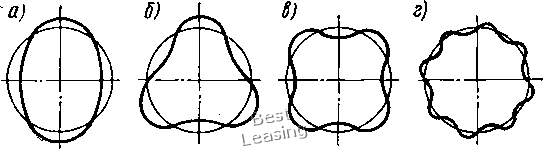

Рис. 1.12. Элементарные виды некруглости цапфы: а - овальность; б - огранка с трехвершинным профилем; в - огранка с четырехвершинным профилем; г - огранка с многовершинным профилем

ствия смещения центра тяжести, которое в полярной системе координат выражается известной формулой

2я k

COS ф dp ф ==

2л «Р>

Sin ц) dp йц) = 0. (1.51)

о о

о о

Нетрудно убедиться, что условие (1.51) выполняется для всех гармоник, за исключением первой. Интегрирование показывает, что присутствие, первой гармоники вызывает смещение центра тяжести площади сечения по отношению к началу координат, с точностью до величин порядка малости (ri/ro), на величину Гх.

Отметим также, что совмещение полюса Oi с центром тяжести площади сечения необходимо, так как только в этом случае уравнение контура идеально круглого поперечного сечения будет иметь вид г (ф) = Го.

Исходные уравнения и граничные условия. Рассмотрим задачу о движении масляного слоя между вращающейся с постоянной скоростью со некруглой цапфой, несущей статическую нагрузку Q, и цилиндрическим вкладышем длиной / и радиусом/? (диаметром/)). В продольном сечении, имеющем криволинейную координату X = CCiy толщина слоя равна h (рис. 1.13).

Основные допущения:

1) форма поперечного сечения цапфы не зависит от продольной координаты г; 2) смазка несжимаема; 3) силы инерции не учитываются; 4) вязкость постоянная; 5) толщина слоя мала; 6) масло прилипает к цапфе.

При сделанных допущениях задача сводится к решению системы дифференциальных уравнений Рейнольдса, которая в общепринятых обозначениях имеет следующий вид [79]:

др дх

дУх дх

ду dv,

ЕЕ. dz

дУ2 ~dz

ду-ду

(1.52)

Последнее уравнение в этой системе является уравнением сплошности.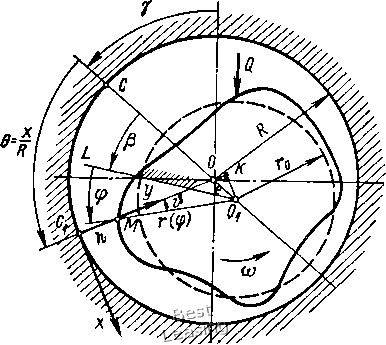

Рис. 1.13. Схема подшипника скольжения с некруглой цапфой

Граничные условия для скоростей:

VxVyv, = 0 при г/ = 0; . I V. = иу = Uy, V2 = Q при y = h.)

(1.53)

Найдем входящие в выражение (1.53) величины /i, и и с учетом некруглости цапфы.

Пусть контур поперечного сечения цапфы описывается выражением (1.49). Введем следующие обозначения: /- = max (гз, з» • • м т); 6 = 7? - Го - средний радиальный зазор; е = rJ8 - относительная некруглость цапфы. Тогда выражение

(1.49) можно представить в виде

г (ф) = г

еб/ (ф).

/ (ф) = 2 "Г ("Р +

k=2 *

(1.54)

(1.55)

известная функция периода 2л.

Поместим начало координат 1г\ в точку 0 равновесия центра круглой цапфы, соответствующую заданной угловой скорости о> и радиусу Го (рис. 1.14). Ось г\ направим к центру вкладыша О. Положение точки 0 определяется эксцентриситетом е = ООд и углом Y между линией действия статической нагрузки Q и линией О2О. Зависимость у = у (е) считается известной [62].

Положение цапфы в системе координат 1г\ определяется координатами и т] центра тяжести цапфы 0 и углом р = со/,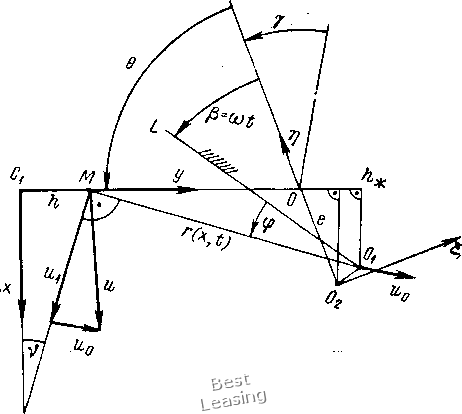

Рис. 1.14. К определению толщины масляного слоя и скоростей точек на поверхности цапфы

образованным координатной осью Т и зафиксированной на цапфе полярной осью OiL. V

Считая перемещения и tj малыми по сравнению с /г и из рис. 1.14 следует, что с точностью до малых величин порядка 8/R

Ф = 0 р = е- со/, (1.56)

где 9 = x/R - текущая угловая координата.

Толщина масляного слоя без учета перемещения центра цапфы (g = 1 - 0) находится из рис. 1.13 и составляет

h=: СгМ= ОСх - {КМ - КО) = 7? - [г (ф) cosiJ - е cos 0], или с точностью до малых величин порядка (б/го)

h = R - г {(р) + е cos Q = 8 + е cos 0 - еб/ (ф). (1.57)

При е = О из последнего выражения получаем хорошо известную формулу для толщины слоя в случае круглой цапфы: /г = б + е cos 6.

Изменение толщины масляного слоя вследствие перемещения центра цапфы определяется по формуле

sin 0 -TjcosG. (1.58)

cos il, у) + r\ cos (т), у)