Подставив (l.llS) в (I.HI), получим формулы для вычисления динамических реакций опор. Результаты вычислений реакции наиболее нагруженной второй опоры представлены в виде графика на рис. Г.25.

Из рисунка видно, что силы инерции снижают динамические реакции на опоры в зоне частот вращения до второй критической скорости (Og- При о) ©з реакция опоры значительно увеличивается. При дальнейшем увеличении со величина R уменьшается и асимптотически стремится к пределу, примерно равному удвоенному значению реакции при со = 0.

Количественную оценку произведем в предположении, что рабочая угловая скорость агрегата равна 50 Гц, или ш - 314 iZ-c. Зная, что каждый ротор имеет

Рис. 1.25. График динамической нагрузки на вторую опору вследствие радиальной несоосности

массу 1470 кг, вычислим р, при котором динамическая нагрузка на опору, отнесенная к половине веса ротора, составляет 1%, или 7,3 кгс. Из графика на рис. 1.25 находим, что при со = 314 1/с

R% = 10-loV кгс/см. Искомая величина составляет р - 0,73 мкм.

Трехопорная конструкция (рис. 1.26, а, б). При радиальной несоосности р ось второго ротора будет совершать коническую прецессию вокруг линии опор О1О3, что эквивалентно появлению эксцентриситета центра тяжести ротора 0,5р.

Максимальная динамическая нагрузка на среднюю опору

Rs km.,p(x>\ (1.116)

где k - коэффициент динамичности системы.

Угловая несоосность роторов ф вызовет появление на стыке валов динамического момента и силы Р:

Нг = /i/(£/im) + i/(3£/i); h, - UI{3Eh)-Динамические нагрузки на опоры определяются по формулам:

(1.118)

77777Г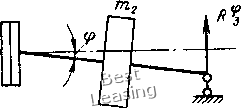

Рис. 1.26. Несоосности в случае трехопорной конструкции агрегата:

а - радиальная; б - угловая

Несоосность в случае гибкой муфты. Методика расчета дина- мических реакций опор в случае гибкой муфты принципиально не отличается от рассмотренного выше случая жесткой муфты, если гибкий элемент целиком отнести к левой полумуфте (рис. 1.27).

Разница заключается лишь в том,, что коэффициенты влияния Ьх-, §1 и hi, входящие в выражение (1.90), должны быть вычислены с учетом радиальной и угловой податливостей гибкого элемента. Это же относится и к коэффициентам б и 7м11 входящим в уравнения (1.106). Все остальные формулы переносятся без изменений.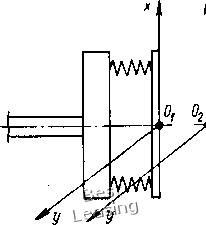

Рис. 1.27. Расчетная схема муфты

гибкой

Податливость гибкого элемента муфты увеличивает указанные коэффициенты влияния. Это приводит к тому, что знаменатель В выражениях (1.95) и (1.Ш1) растет быстрее, чем числитель.

Тем самым нагрузки Р и М и динамические реакции опор уменьшаются.

Следует отметить, что недостатком гибкой муфты является возможность появления несоосностей роторов в результате пере-меш.ен и я осей опор.

5. Влияние температурной асимметрии роторов машин на их виброактивность

Рабочие процессы, происходяш,ие во многих роторных машинах, вызывают неравномерное распределение температуры по объему ротора. Возникающие при этом термоупругие деформации могут быть причиной искривления продольной оси и появления температурного эксцентриситета центра масс ротора.

Теория температурных прогибов балок достаточно полно изложена в работе Б. Боли и Д. Уэйнера [19]. Здесь приведем лишь основные положения этой теории без доказательств. Затем рассмотрим основные закономерности появления температурных прогибов тел вращения на примере сплошного цилиндра. Далее полученные результаты перенесем на конкретные роторные конструкции.

Основные положения теории температурных прогибов балок.

При расчетах температурных напряжений и прогибов балок используется гипотеза Бернулли-Эйлера, согласно которой сечения, плоские и перпендикулярные к осевой линии до температурного нагружения, остаются плоскими и перпендикулярными и после нагружения, и влиянием поперечной деформации можно пренебречь.

Предполагается также, что балка статически определима и свободна от внешних нагрузок; поперечное сечение имеет произвольную форму и не является постоянным; распределение температуры произвольное.

Введем следующие обозначения: х - осевая координата балки; у, Z -г центральные оси в плоскостях поперечных сечений; 5 (х) - площадь поперечного сечения балки; 1, -моменты инерции площади поперечного сечения относительно соответствующих осей;, - центробежный момент инерции; Е - модуль упругости материала балки; а - коэффициент линейного расширения; Т (х, у, г) - температура балки; у, w - прогибы оси балки в направлениях у \ z соответственно.

Тогда дифференциальные уравнения изогнутой оси балки под действием температурного поля Т (х, у, z) имеют следующий вид [191:

(1.119)

aETzdS; Мтг

aETy dS,

(1.120)

(S) (S)

В частном, случае главных осей {1 = 0) уравнения (1.119) упрощаются и принимают вид:

dv Мтг сс

dx dw

Мту Ely

TydS]

Tz dS.

(1.1,21)

Температурные прогибы v и w находятся путем интегрирования уравнений (1.119) или (1.121) при заданных граничных условиях.

Условие отсутствия температурных прогибов имеет вид:

Ту dS

TzdS = 0.

(1.122)

. (S) (S)

Так как координатные оси центральные, то

zdS = 0,

и из выражения (1.122) следует, что температурное поле вида Т Tq + Ti (х) прогибов не вызывает.

Необходимо отметить, что приведенные здесь формулы дают прогибы балки, свободной от внешних нагрузок. При таких нагрузках их влияние можно вычислить отдельно и затем соответствующий результат наложить на полученные здесь решения.

Решения для статически неопределимых балок можно получить также путем наложения решений, найденных для раздельно действующих нагревания и реакций опор.

Температурные прогибы цилиндра. Рассматривается цилиндр радиусом г (диаметром d), длиной/и имеющий заданнукг температуру поверхности.

Будем считать, что длина цилиндра значительно больше его диаметра. Такое предположение позволяет пренебречь влиянием торцового теплообмена и свести задачу определения температуры в цилиндре конечной длины к более простой задаче для неограниченного цилиндра.

Распределение температуры в цилиндре определяется решением уравнения Лапласа, которое в цилиндрической системе координат р, 9, X имеет вид:

1 дТ дТ . (1123)

I дТ

9 др

Граничные условия:

Т = Ti (9, х) при р = г.

4 А. с, Кельзои и др.

(1.124)

Разложим функцию Ti (9, х) в ряд Фурье

Ti (9, X) (ср„ (х) cos nQ + гз„ (х) sin п9

(1.125)

2я .

Т, (9, X) d9; ф„ (X) -

ri(9, x)cos/i9d9;

Ф/г ()

ri(9, X) sin riQde,

Дальнейший вывод решения можно найти, например, в работе [41]; здесь приведем лишь окончательный результат:

оо оо

Ф) sin/i9}e~slP-«l dp,

Ф„ (p) cos„ 9

(1.126)

где Jn (z) - функция Бесселя n-ro порядка 1-го рода; (s = = 1, 2, ...) - положительные корни уравнения (га) = 0.

Для получения обозримых результатов рассмотрим два частных случая распределения температуры поверхности цилиндра, представляющие наибольший интерес.

Температура поверхности зависит от угловой координаты 6 и является линейной функцией продольной координаты х. Пусть

Г - Ti (9) + хТ (9) при р - л

(1.127)

где Ti (0) и Г2 (0) - произвольные функции угла 9, разложения которых в ряд Фурье имеют следующий вид:

i(9) Л (a„Gos/z9 + b„sin/i9);

00 ч

Т2 (9) = 1j {Лп cos nQ + Вп sin п 9).

(1.128)

Тогда, сравнив формулы (1.125) и" (1.128), получим: • (f,(x) = a,, + A,xi yp,{x)=b, + B,x (/г-0, 1, 2,...). (1.129) Использовав приведенное в работе [41] равенство

2 y Jn(pas(j y („0. 1,2,,...),

а также, учтя, что

а,

после подстановки (1.129) в (1.126) получим

Г(р, 9, х)= 2 (~-)"[K + 4)cosn9 + (l?„ + B„x)sin/?9].(1.130)

Температура поверхности зависит только от угла в. Пусть

Т =Тг (0) при р = г, (1Л31)

где Ti (0) - функция, имеющая разложение в ряд Фурье вида (1.128).

Искомое распределение температуры получается из выражения (1.130) при = В„ О и имеет следующий вид:

Г(р, 0)= 2 (-)"(«cos/i0 + b„sinn0). (1.132)

Перейдем теперь к определению прогибов оси цилиндра под действием температурных полей (1.130) и (1.132). При расчетах примем, что цилиндр свободен от внешних нагрузок и концы его шарнирно оперты.

Пусть в цилиндре установилось температурное поле (1.131)- (1.132), (рис. 1.28, а).

Тогда, учитывая формулы:

р cos 0; г = р sin 0; dS = р ф d0,

вычисляем интегралы (1.120):

2я г

Ту dS

Т (р, 0) р2 cos 0 dp dQ

cos 0

2 (С05/г9 + -81пп9)]р«+2ф

3X1 r

2я r

TzdS =

Г(р, 9)p"sln9<ipc(9

0 0

Подставив найденные значения интегралов в (1,121), получим дифференциальные уравнения изогнутой оси цилиндра:

aai , dw

dx r dx r

Граничные условия имеют вид:

V w = О при X = О и X = /.

(1.133)

(1Л34) 51