Пример 2.9. Решить уравнение Лапласа

ixx + Uyy = 0, - оо<а:<оо, у>0,

с заданными при у = 0 граничными условиями и{х, 0) = 0,

Uy (л:, 0) = (1/п) sin (пх), д > 0.

Решение. При помощи метода разделения переменных легко получить

и = (l/n) sin (пх) sh (пу).

Если рассматриваемая задача корректно поставлена, решение должно непрерывно зависеть от граничных условий, одно из которых имеет вид

Uy{x, 0) = (1/п) sin (да:).

Следовательно, при больших п величина Uy малая. Решение уравнения ведет себя при больших п иначе. При больших п решение и стремится к е/п, т. е. неограниченно растет даже

при малых у. Однако и{х,0)=0, т. е. непрерывность по начальным данным отсутствует. Итак, задача поставлена некорректно. К этому же выводу можно было прийти на основе проведенного выше анализа свойств уравнений в частных производных, не выписывая их решение. Действительно, уравнение Лапласа эллиптическое, поэтому его решение зависит от условий на всей границе замкнутой области. В рассмотренном же примере требовалось найти решение эллиптического уравнения в открытой области, так как граничные условия были заданы лишь на линии у = 0.

Наиболее часто встречающимся краевым задачам для уравнения Лапласа присвоены имена известных ученых. Первой укажем задачу Дирихле (рис. 2.8), в которой требуется найти решение уравнения Лапласа в замкнутой области, если на ее границе задано значение искомой функции. В задаче Неймана также надо найти решение уравнения Лапласа в замкнутой области D, если на ее границе задана производная искомой функ-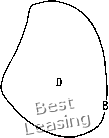

Рис. 2.8. Задача Дирихле: = О в D, u=f{x) на В.

Vu = 0 в области D,

1М"1 + а2{х)и = h(jc) на границе В.

Эту краевую задачу иногда называют также третьей краевой задачей для уравнения Лапласа [Zachmanoglou, Thoe, 1976] или задачей Робина. Часто именем Дирихле, Неймана и Робина называют тип граничных или начальных условий, заданных для любого уравнения в частных производных. Например, если мы говорим: «граничное условие Дирихле», то это значит, что на границе области задано значение искомой функции. Такая терминология используется для уравнений в частных производных любого типа.

§ 2.5. Системы уравнений

При изучении физических процессов обычно приходится решать системы уравнений в частных производных, так как редко удается описать сложный физический процесс одним уравнением в частных производных. Но даже в тех случаях, когда физический процесс описывается одним уравнением в частных производных высокого порядка, это уравнение можно заменить системой уравнений первого порядка. Проиллюстрируем это двумя простыми примерами.

Заменим волновое уравнение (2.32) системой двух уравнений первого порядка. Обозначим

ди ди

И рассмотрим систему уравнений

ду dw

dt дх

dt дх

ции ПО нормали к В, а не сама искомая функция: Vu = 0 в Д -j = g(x) на В.

Обобщением задач Дирихле и Неймана, когда на границе замкнутой области задана линейная комбинация искомой функции и ее производной по нормали к границе является так называемая смешанная краевая задача:

дх ди

(2-46)

ду дх

относительно неизвестных w и и. Это известные уравнения Коши - Римана [Churchill, 1960], широко используемые в теории конформных преобразований).

Так как многие задачи вычислительной гидродинамики сводятся к решению систем уравнений в частных производных первого порядка, то для корректной постановки задач необходимо уметь определять тип системы уравнений в частных производных. Рассмотрим систему линейных уравнений в частных производных первого порядка

l + H]f- + fB]H. + r = 0. (2.47)

Для простоты ограничимся случаем, когда матрицы коэффициентов [А] и [В] являются функциями только t, X и у. Неизвестное U является вектором-столбцом, а г зависит от и, х и у.

С точки зрения авторов работы [Zachmanoglou, Thoe, 1976] тип системы уравнений в частных производных первого порядка можно уверенно определить лишь в двух случаях. Система уравнений (2.47) называется гиперболической по (л:, t), если все собственные значения матрицы [А] вещественны и различны. Рихт-майер и Мортон [Richtmyer, Morton, 1967] предложили считать гиперболической систему уравнений в том случае, когда все собственные значения матрицы [А] вещественны и эту матрицу можно представить в виде [Т] [%] [Т]-\ где [К] - диагональная матрица, состоящая из собственных значений матрицы [Л], а матрица [Г]- матрица левых единичных собственных векторов. То же самое можно сказать о поведении системы уравнений по (yj) в зависимости от собственных значений матрицы [В].

Следует отметить, что между решениями уравнения Лапласа и уравнений Коши -Римана существует некоторое различие: решение уравнений Коши-Римана всегда является решением уравнения Лапласа, но не всякое решение уравнения Лапласа является решением уравнений Кощи -Римана,

Подставляя в любое из уравнений вместо w и v их выражение через Uy видим, что функция и удовлетворяет волновому уравнению.

Многие физические процессы описываются уравнением Лапласа (2.1). Заменим его системой уравнений в частных производных первого порядка

ди dv