h. Это легко показать, считая 5 расстоянием, измеряемым вдоль характеристики, и записывая

tf»-») = i»"rv)t + i»«-»).

Однако если {и - v) постоянна вдоль характеристики, то можно записать

(Р»-») + (-)»«-») = о.

что есть не что иное, как уравнение (6.17а). Таким образом, мы приходим к выводу, что (ра - v) постоянна вдоль характеристики, отвечающей собственному числу а величина (u-\-v)

sin(27rf)

Рис. 6.2. Волнистая стенка в виде одного периода синусоиды.

постоянна вдоль характеристики ?i2. Величины (Рг/- v) и (рг/+у) называются инвариантами Римана (см. [Garabedian, 1964]). Так как эти две величины постоянны на распространяющихся в противоположные стороны характеристиках, легко определить и и V в заданной точке. Если величины {и -\- v) и {и - v) известны в некоторой точке (л:, у), мы сразу же находим и и v в этой точке. Рассмотрим пример расчета по методу характеристик.

Пример 6.1. Однородное сверхзвуковое {М. = л/2 ) течение невязкой жидкости в ударной трубе натекает на неровность стенки в виде одного периода синусоиды. Такая конфигурация изображена на рис. 6.2. Амплитуда синусоиды равна е и г/L < < 1. Определить возмущенные скорости и и v, используя метод характеристик.

дх ду

= 0,

dv Q

дх ду С начальными условиями

и = 0, v = 0 вдоль л: = О, у> О и граничными условиями, заданными на стенке (см. § 6.4):

и = 2я -р- cos (2я , О < л: < L.

Так как задача двумерная и решается в рамках теории малых возмущений, можно перенести граничные условия на плоскость у = 0. Это во многом облегчает задачу.

Начнем с того, что нарисуем характеристики, берущие свое начало на поверхности задания начальных данных х = 0. На левой характеристике

dy/dx = 1, u - v = P = const, тогда как на правой характеристике

dy/dx = --1, u-\-v = Q = const. Следовательно, мы определяем и и v в любой точке:

r/ = (P + Q)/2, v = {Q-P)/2.

Так как правые характеристики, пересекающие поверхность, исходят из невозмущенного потока, то начальное значение переменной Q равно нулю. Кроме того, Р = О для характеристик, исходящих из невозмущенного потока (рис. 6.3).

Рассмотрим характеристики, которые пересекают волнистую стенку. Распространяющаяся вверх, или левая, характеристика приходит в некоторую точку так, что приносит в нее граничное условие с поверхности волнистой стенки, т. е. в некоторой точке xi мы имеем

Q = u + v = 0, и = соз(2я), Следовательно,

и =--J-2- cos

Решение. Так как течение по условиям задачи отвечает требованиям о малости возмущений, то при решении задачи можно пользоваться уравнением Прандтля - Глауэрта. Итак, будем решать систему уравнений (6.3) для возмущенных компонент скорости и и V. В этом случае Рг = 1 и система выглядит так:

ди dv

312 Гл. 6. Численные методы решения уравнений течения

P=.„-, = -i=-cos(2n).

Решение для и и v строится в соответствии с маршевой процедурой по направлению х, исходя из плоскости задания начальных данных. На рис. 6.4 показана сетка с нумерацией узлов

Р = и-и=0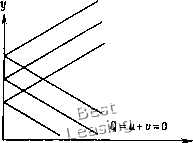

Рис. 6.3. Линия задания начальных данных.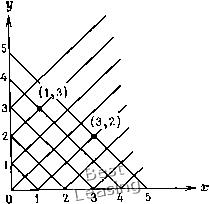

Рис. 6.4. Расчетная сетка, узлы которой являются точками пересечения характеристик.

И соответствующие характеристики. Теперь на пересечении характеристик мы можем получить решение. В точке (1,3)

р = 0, Q = 0, г/ = 0, v = 0,

В точке (3, 2)

Р = -со8(2я). Q = 0,

= со8(2я), t; = cos(2n).

Таким образом, мы получили решение во всей интересующей нас области. Оно может быть проверено непосредственным решением уравнения Прандтля - Глауэрта для потенциала скорости, по которому затем находят и и v.

6.2.2. Нелинейные системы

До сих пор мы рассматривали систему из двух линейных уравнений, которая была выбрана ради простоты. В более сложных нелинейных задачах решение получают уже не так легко.