1975] (см. п. 4.1.9) и использованной Стегером и Уормингом [Steger, Warming, 1979]. Схема Бима - Уорминга второго порядка на шаге предиктор совпадает с уравнением (6.102), а шаг корректор задается как

wr = w? + (w? + wr) +

+ Aw? -[АГ vV. (6.105)

Введенные на шаге корректор два дополнительных члена изменяют ошибку аппроксимации так, что схема дает второй порядок точности, удовлетворяя при этом условию сдвига.

Процедуры постановки граничных условий в методах, подобных методу расщепления матричных коэффициентов, имеют разумное обоснование. На границах вычислительной области некоторые характеристики приходят к границе из внутренней части, другие -извне. Мы можем воспользоваться уравнениями совместности вдоль характеристик, приходящих к границе из внутренней части области. Однако информацию, приносимую остальными характеристиками, использовать невозможно. Соответствующие соотношения совместности должны быть заменены заданными граничными условиями. Это могут быть либо условие скольжения потока вдоль твердой границы, либо заданные распределения давления или скорости на внешней границе. При рассмотрении сверхзвуковых течений с ударными волнами ударные волны следует трактовать как разрывы. Это будет обсуждаться позже в данной главе.

Пример 6.5. Пусть требуется рассчитать распределение давления в одномерном сопле, когда первоначально покоящийся газ разгоняется до скорости звука в горловом сечении, а затем расширяется в сверхзвуковой части сопла при заданном давлении на срезе сопла. Схематически сопло изображено на рис. 6.14.

Решение. Одномерное течение газа описывается следующей системой уравнений:

дР , дР , (ди , \

ди ,- , п dt дх у дх

где а ={1/А)дА/дх. Так как мы пользуемся недивергентной формой записи уравнений, то правильно «поймать» скачок внутри сопла нельзя. При интегрировании уравнений (6.106) необходимо иметь уравнение для энтропии или считать поток изэнтропическим (s = const). В нашем примере для простоты будем

считать энтропию постоянной. Даже в рамках этого предположения единственное решение для течения в сопле получаем интегрированием уравнений по времени.

Соответствующая форма уравнений с расщепленными матричными коэффициентами без труда получается из уравнений (6.106), и ее вывод здесь мы приводить не будем. Сосредоточим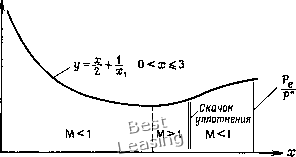

= 0.75

Рис. 6.14. Одномерное течение в сопле.

наше внимание на постановке граничных условий на срезе сопла. На рис. 6.15 показан срез сопла и приходящие на него характеристики в плоскости (xj). Поскольку характеристики, имеющие

Срез сопла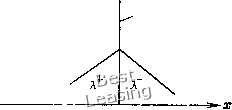

Рис. 6.15. Характеристики в плоскости среза.

отрицательный наклон, приходят извне, то соотношение совместности на них следует заменить граничным условием. В нашем примере это р = 0.75р*, где р* -давление заторможенного потока. Уравнение совместности вдоль характеристики с положительным наклоном дает полезную информацию, которой мы и воспользуемся. Оно записывается в виде

дР dt

+ Y4r + 4lr+V-§) + Yaal/ = 0. (6.107)

Для заданного давления на срезе сопла требуем, чтобы dP/dt = 0. Когда производные по л: в уравнении (6.107) аппроксимируются разностями назад, новое значение скорости на срезе сопла получается сразу интегрированием. Оно вместе с заданным на срезе сопла давлением полностью определяет задание граничных условий на срезе сопла.

Метод расщепления матричных коэффициентов применим в случае любого числа измерений, и в этом плане поучительным является пример двумерного зависящего от времени течения. Обычно выполняется преобразование координат

т = /, l = {ty X, у), л = Л( X, у).

(6.108)

Если в декартовой системе координат переменными являются 5, и, V и Ру то в преобразованных координатах уравнения запишутся в виде

Wx + [А] wg + [В] W, + h = 0. (6.109)

В соответствии с принятыми ранее обозначениями мы можем расщепить матрицы [А] и [В]; тогда получим

W, + [Т] [Лл] [ТГ + [S] [AsUSr w, + h = 0. (6.110)

В этом выражении [Лл] и [Лв] -диагональные матрицы, состоящие из собственных значений матриц [А] и [В], а [Т]- и [S]- - транспонированные матрицы, составленные из соответствующих собственных векторов. В уравнении (6.110)

w = (5, г/, и, ру,

h = (0. О, О, 8уУ,

(6.111) (6.112)

где 8 =(1,0) для осесимметричного или двумерного течения соответственно.

[А] =

(6.113)

[Л]-диагональная матрица с элементами

ы, ы и (6.114)