иЩМ. (6.159)

Это дает положительную искусственную вязкость, когда

UyA>al (6.160)

Последнее условие должно быть выполнено, если решается мар- шевая задача для уравнения потенциала в случае сверхзвукового течения. Если условие (6.160) не выполняется, искусственная вязкость становится отрицательной и это ведет к неустойчивости. Отметим, что возникающие в уравнении (6.157) смешанные производные аппроксимируются разностями против потока, зависящими от знаков коэффициентов при них, чтобы обеспечить преобладание диагональных членов в случае неявной схемы. Производная по г\ для уравнения потенциала вычисляется в точке I + 1:

(T)=i[M.*.+wL,,.

ЧТО приводит к неявному алгоритму по маршевой координате. Если это разностное выражение записать через разность потенциалов А, то

dr\\fj~\ J Л "Т" V / (?ч Л V J дг\

(6.161)

где Р?ц. - плотность на п-й итерации в точке сетки f + 1- На каждом шаге при продвижении по g новое значение плотности должно определяться путем итераций. В большинстве задач оказывается, что этот процесс состоит из одной-двух итераций. Чтобы корректно ввести искусственную вязкость, шаблон при аппроксимации плотности смещается против потока (см. [Hoist, 1979; Hafez et al., 1979]). Значение pfj в уравнении (6.161) заменяется выражением

(6.162)

Если используется конечно-разностная аппроксимация первого порядка против потока

4г:=[( к,1 (6.158)

ТО главный член ошибки аппроксимации есть

+ 1, К/ + 1./ + 1/2 <0,

v,+b/+i/2 = [l~(ivpryi » (6.163)

причем 5 = 0 для Vi+i, /+j/2 > О и 5 = 1 для Vi+u ж/2 < 0. Такое представление плотности [уравнения (6.162) и (6.163)] вводит положительную искусственную вязкость во всех точках, где М?+1 > 1 (скорость потока сверхзвуковая). Поскольку мы рассматриваем маршевую процедуру решения уравнения потенциала для сверхзвуковых течений, то метод оказывается несостоятельным, когда поток дозвуковой и искусственная вязкость становится отрицательной.

Чтобы найти решение на слое /+ 1, зададим на нем неявные граничные условия. В любой плоскости симметрии можно воспользоваться простым отражением. Например, в двумерной задаче, когда делают проход по направлению г), можно ставить это условие на границе (считаем, что симметричные граничные условия мы имеем при / = /max - 1), задавая

(W..w = (AU..W-2. (6.164)

Постановка граничных условий на поверхности тела почти такая же простая. Если система координат предполагается адаптированной к поверхности тела, то в двумерном случае на поверхности тела можно задавать условие типа

Для задания. граничных условий на поверхности (/ = 2) тела можно воспользоваться фиктивной точкой (/= 1), расположенной под поверхностью. Пусть

0 = ViU2 = А,У) + А,--.

(6.165)

Это выражение используется для исключения из уравнения на границе значения функции в фиктивной точке (/= 1). В расчете с неявным граничным условием отсутствует ограничение на размер шага по маршевой координате, которое может возникнуть из-за наличия границы. К тому же неявное задание граничных условий ускоряет сходимость итерационного процесса нахождения плотности на каждом шаге по .

- 1, Vi + l, /+1/2 > О,

В конечном счете процесс вычислений сводится к решению трехдиагональной системы уравнений для Д. В этом легко убедиться, рассматривая систему, записанную в виде

С, д

где Ci, С2, Сз и р - коэффициенты при членах с производными, а R - известная правая часть уравнения. В качестве упражнения читателю предлагается найти выражения для этих членов

0,35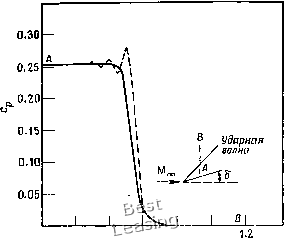

0.2 О.А 0.6 U.8 1.0

Расстояния от поверхности

Рис. 6.23. Решение уравнения потенциала для обтекания клина; нение полного потенциала (скаляр);---уравнения Эйлера.

урав-

(см. задачу 6.15). Решая трехдиагональную систему, находим Д. Зная Д, вычисляем р/+1. Это новое значение плотности используется для расчета новой величины Д из уравнения (6.166), и этот итерационный процесс повторяется, пока не будет достигнута сходимость. В трехмерном случае следуют той же процедуре с той лишь разницей, что решение для Д получают, используя приближенную факторизацию, что требует решения трехдиагональных систем по направлениям т] и .

Шанкар и Ошер [Shankar, Osher, 1982] применили описанную выше процедуру для решения уравнения полного потенциала. Вместо простой линеаризации плотности по уравнению (6.155) здесь разлагают в ряд произведение плотности и контра-вариантной компоненты скорости по направлению g в виде

(pt/)+i = (pf/)/ + A(pf/)-