и является высокоэффективной процедурой расчета трансзвукового обтекания профилей, будучи объединенной с процедурой построения сетки. Кроме того, эту схему можно использовать и для расчета трехмерных конфигураций. Холст [Hoist, 1980] распространил свой подход на расчеты обтекания трехмерных

-1,2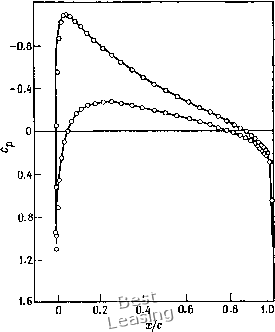

Рис. 6.28. Распределение коэффициента давления Ср на профиле NASA 0012;

а = 2 Моо = 6.63; О Сь = 0.334 [Hoist, 1979]; - Cl = 0.335 [Lock,

1970]. . --Щ

Крыльев. Его процедура является дальнейшим развитием двумерного метода.

Следует отметить особо один очень важный момент. В двумерном случае использование схемы, в которой шаблон при аппроксимации плотности сдвигается назад по направлению , оказывается достаточной мерой. Если сверхзвуковой поток достигает задней кромки, то и в направлении у\ также необходимо использовать разности против потока. В трехмерных расчетах обтекания крыльев разности против потока используются и в направлении размаха крыла, и в направлении хорды. Если сверхзвуковые области возникают вблизи задней кромки, разности

§ 6,6. Уравнения малых возмущений для трансзвуковых течений 371

против потока необходимо использовать и в нормальном направлении.

В работе [Hafez et al., 1979] указано, что члены с искусственной вязкостью, возникающие при разностном представлении плотности разностями против потока, можно рассматривать как аппроксимации уравнений Навье -Стокса. Было получено вязкое трансзвуковое уравнение малых возмущений [Sichel, 1963]

(1 -М2),, + <,= -8,,,. (6.179)

Здесь вязкие члены имеют ту же форму, что и искусственная вязкость, добавленная в сверхзвуковых областях явным образом, или искусственная вязкость или искусственная сжимаемость, вводимые за счет модификации разностного представления плотности.

И последнее замечание по поводу уравнения полного потенциала. Стейнхофф и Джеймсон [Steinhoff, Jameson, 1981] сообщают, что были получены неединственные решения уравнения потенциала в случае трансзвукового течения. В этих расчетах число Маха изменялось в диапазоне от 0.82 до 0.85 и задача обтекания профиля Жуковского с толщиной 11.8% имела более одного решения при данных условиях. В этом есть что-то настораживающее, и должны быть предприняты дальнейшие исследования численных решений уравнений Эйлера и уравнений Навье-Стокса для таких условий. Это позволит ответить на вопрос, является ли неединственность свойством уравнения полного потенциала или это физическое явление. Предварительное изучение уравнений Эйлера, по-видимому, говорит в пользу первой гипотезы.

§ 6.6. Уравнения малых возмущений для трансзвуковых течений

В предыдущем разделе речь шла о расчетах трансзвуковых течений невязкой жидкости при помощи уравнения полного потенциала. Результаты, полученные для профилей и некоторых трехмерных конфигураций, очень хорошо согласуются с имеющимися экспериментальными данными. Методы решения уравнения полного потенциала очень эффективны, поэтому они широко применяются. Известно, однако, много случаев, когда нет необходимости решать уравнение для полного потенциала, и достаточно точности, которую обеспечивает решение уравнения малых возмущений. К тому же простота постановки граничных условий делает его применение еще более привлекательным. В двумерном случае граничные условия ставят на линии разреза, в трехмерном - на плоскости. Уравнения существенно упрощаются, так как отпадает необходимость отображения об-

ластей сложной формы на более простые для удобства постановки граничных условий. Это в свою очередь приводит к тому, что потребности в ресурсах ЭВМ (процессорное время и память) значительно уменьшаются, особенно в трехмерных задачах.

Трансзвуковое уравнение малых возмущений можно получить применением процедуры разложения в ряд [Cole, Messiter, 1957; Hayes, 1966], что дает возможность систематическим образом получать приближения уравнений Эйлера все более высокого порядка. В гл. 5 трансзвуковое уравнение малых возмущений (5.203) было выведено в предположении малости возмущений. В безразмерной форме его можно записать в виде

[/С - (Y + 1) Фх] Фхх + Фуу = О, (6.180)

где /С -параметр подобия:

= (1-М2)/б2/3; (6.181)

здесь б - максимальная относительная толщина профиля и / - функция формы профиля, оцределяемая выражением

у = бПх). (6.182)

Потенциал скорости в уравнении (6.180) - возмущенный потенциал, определяемый так, что производная по л: есть возмущенная скорость по координате л:, обезразмеренная по скорости набегающего потока и параметру подобия по направлению у. Масштабированная координата у определяется так:

у = 6у. (6.183)

Уравнение (6.180) формально эквивалентно уравнению (5.203), и оба они являются разновидностями трансзвуковых уравнений малых возмущений Гудерлея - Кармана. Уравнение (6.180), куда входит параметр подобия Ку через который выражаются законы подобия, было использовано Мёрменом и Коулом [Миг-man. Cole, 1971] для расчета обтекания невязкой жидкостью профиля с нулевой подъемной силой. Коэффициент давления определяют так же, как и в случае уравнения (5.205), тогда можно записать Ср = -2фх. Для течений, которые нельзя считать трансзвуковыми, мы получаем уравнение Прандтля - Глауэрта для до- и сверхзвуковых течений. Оно уже не раз приводилось в предыдущих главах и выглядит так:

{-1)Фхх + Фуу = (6.184)

Основная его особенность в том, что оно нелинейно и меняет свой тип от эллиптического к гиперболическому, как и уравнения Эйлера, и уравнение полного потенциала.