практических конфигураций быстродействие и память современных ЭВМ позволяют это делать. Однако для получения хорошего решения существенны адекватный выбор количества панелей и их расположение на поверхности.

При изучении панельных методов будем рассматривать безвихревое течение невязкой несжимаемой жидкости, которое описывается уравнением Лапласа для потенциала скорости. Потребуем

V2 = 0 (6.189)

и зададим на границах рассматриваемой области либо фу либо дф/дп. Для простоты ограничимся рассмотрением двумерного

У У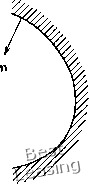

Рис. 6.31. Физическая область для уравнения Лапласа.

случая, хотя принципиально он ничем не отличается от трехмерного. Рассматриваемая область изображена на рис. 6.31. В основе всех панельных методов лежит замена решения уравнения Лапласа в рассматриваемой области некоторым поверхностным интегралом за счет применения второй формулы Грина к интересующей нас области. Пусть функции и v имеют непрерывные производные вплоть до производных второго порядка (функции мну принадлежат к классу С"), тогда вторая формула Грина может быть записана в виде

J J (ttVt; - \ ~"

где n -единичная нормаль к границе и /-элемент дуги вдоль границы. Выберем в качестве и потенциал , а в качестве v -

функцию вида о = 1п (г), где г = - 5) + (У - л). Пусть (I, т])-координаты точки Р, в которой следует определить потенциал, а (л:, у)-координаты точки Q на границе, в ко-

<l>il.r,) = -iJ[lnir)f-f]ds. (6.190)

Таким образом, решение уравнения Лапласа в некоторой области мы свели к задаче решения интегрального уравнения на границе этой области. Первый член соответствует задаче Неймана, в которой на границе задается дф/дп, второй - задаче Дирихле с краевым условием, когда на границе задается ф. Интегралы в равенстве (6.190) дают вклады в от источников и диполей. Далее можно записать

где а можно интерпретировать как плотность распределения источников, а \л - плотность распределения диполей с осью, перпендикулярной к поверхности границы.

Поверхностное распределение источников с плотностью or на

торой расположен источник. При вычислении интегралов в формуле Грина следует быть особенно внимательным по мере приближения точки (I, т)) к (л:, у), т. е. когда Чтобы избежать связанных с этим обстоятельством трудностей, вообразим, что вокруг точки РЦуЦ) построена окружность малого радиуса и применим формулу Грина к области, заключенной между границей В рассматриваемой области и этой малой окружностью. Имеем

О = {vVu - uVv) -nds - {vVu - uVv) • n ds. в e

Bo втором интеграле заменим и и v их зависимостями от и г:

([1п (г) V-V ln(r)].nrf5.

На окружности малого радиуса г равно е, и этот интеграл можно записать в виде 1п (е) ф • п rfs - § 7 ds. В соответствии с нашим исходным предположением о том, что ф есть решение уравнения Лапласа, первый член обращается в нуль (см. задачу 2.7).

Второй член есть гфds, но по известной теореме о среднем

значении гармонической функции он равен eфds = 2лф{l, г\).

Подставляя последнее равенство в исходное выражение, получаем

/=1 /

Of In {гij)dsj. (6.193)

Аналогичное выражение можно получить и для распределения диполей. Если в области, где имеются п панелей с распределенными источниками, существует еще и однородный поток, то с учетом его потенциала записываем

Наиболее простое и удобное для проведения численных расчетов выражение получают в случае, когда интенсивности источников панелей полагаются постоянными. В более совершенных методах пользуются другими распределениями, и тогда выражение для потенциала скорости становится более сложным. Для постоянной интенсивности источников на панели имеем

h = их, + 5] 5 1п inj) ds,. (6.195)

Геометрия области, соответствующая такому распределению потенциала, показана на рис. 6.32. Далее необходимо определить интенсивности источников о/. Для этого на каждой панели выбирают контрольную точку и требуют, чтобы через панель поток отсутствовал. Контрольную точку выбирают в центре панели. Пусть точка Р является контрольной точкой i-й панели. Условие отсутствия перетекания через панель в этой точке есть

ж;Ф(ьУ1) = о. (6.196)

Так как ф - потенциал скорости, то это равенство просто выражает факт обращения в нуль нормальной скорости в контрольной точке /-Й панели. Таким образом,

Е-15г$"М/ = -1-" (6.197)

/=1 /

единицу длины дает во внешней точке величину потенциала

Ф = §а1п{г)а8у (6.192)

где интегрирование производится по всей поверхности. Если мы имеем п поверхностей или панелей, суммарный потенциал в точке Р есть сумма вкладов от каждой панели: