вать в ряд Тейлора в одной и той же точке. При таком подходе к построению разностной схемы погрешность аппроксимации уравнения в частных производных равна сумме погрешностей аппроксимации его членов.

Разложение функций в ряд Тейлора не обязательно проводить в узле {/, •/) разностной сетки. Проиллюстрируем это двумя примерами. Используемые при построении конечно-разностной аппроксимации производных узлы разностной сетки (шаблон) и

.1-1

J>1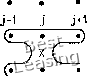

Рис. 3.4. Шаблон, используемый при решении уравнения теплопроводности по неявной схеме; крестиком указана точка, в которой проводится разложение в ряд Тейлора.

Рис. 3.5. Шаблон, используемый при решении уравнения теплопроводности по схеме Кранка - Николсона; крестиком указана точка, в которой проводится разложение в ряд Тейлора.

точка, в которой проводится разложение функций в ряд Тейлора, показаны на рисунках.

Полностью неявная разностная схема для уравнения теплопроводности (3.55) имеет вид

(3.70)

погрешность аппроксимации схемы равна 0[А, (Ах)2]. Используемый шаблон и точка (д + 1,/), в которой удобнее всего проводить разложение функции в ряд Тейлора, показаны на рис. 3.4.

Схема Кранка - Николсона для уравнения теплопроводности тогда имеет вид

(3.71а)

погрешность аппроксимации схемы 0[{At), (Ах)]. Используемый шаблон и точка (ai+ 1/2,/), в которой удобнее всего проводить разложение решения в ряд Тейлора, показаны на рис. 3.5.

Интересно отметить, что погрешность конечно-разностной аппроксимации всего уравнения в частных производных (но не его отдельных членов) не зависит от выбора точки, в которой проводится разложение решения в ряд Тейлора. Покажем это на примере схемы Кранка - Николсона. Обычно погрешность аппроксимации для этой схемы определяют путем разложения решения в ряд Тейлора в окрестности точки (az-f 1/2, /). Использование этой точки приводит к исключению максимального числа членов из разложения Тейлора путем сокращения. Покажем, что при разложении решения в ряд Тейлора в окрестности точки (ai,/) или даже точки (ai-1,/) погрешности аппроксимации не изменятся. Для этого мы должны весьма тщательно проанализировать погрешность аппроксимации. Разложим функции

jLp "/+1» /"*" в ряд Тейлора в точке (ai,/); после

несложных преобразований из (3.71а) получим

щ - аи,, = Utt- + ащ,, f - + О (Аа:)-f О {Mf. (3.71b)

Так как в правую часть этого уравнения входят члены -uttA.t/2 и aUixxAt/2y то на первый взгляд кажется, что погрешность аппроксимации уравнения равна 0{At) + 0{Ах). Однако сумма указанных членов равна -At/2{d/dt)(ut - auxx)y где под знаком производной стоит левая часть уравнения (3.71Ь). Продифференцировав (3.71Ь) по t и умножив обе части полученного уравнения на -At/2, получим

- А/2 id/dt) {щ ~ аих) = О (А/)2 + О {АхУ.

Следовательно, погрешность аппроксимации уравнения теплопроводности при использовании схемы Кранка - Никольсона равна 0{Aty+0{Axy независимо от того, в какой точке проводится разложение функций в ряд Тейлора: (ai+1/2,/) или (az,/). Порядок аппроксимации уравнения не изменится при разложении функций в ряд Тейлора в окрестности любой другой точки. Рассмотренный пример показывает, что при анализе точности разностной схемы необходимо тщательно проверить, не являются ли коэффициенты при главных членах в выражении для погрешности аппроксимации произведением некоторой функции на производную исходного дифференциального уравнения. Если это так, то для определения погрешности аппроксимации необходимо рассмотреть члены более высокого порядка.

= 0. -

. = -д

= 2с.

Коэффициенты а, 6, с можно определить, зная температуру в конкретных узлах сетки и шаг сетки Ах. Для этого сначала надо выбрать используемые при интерполяции средние узлы разностной сетки, т. е. задать геометрическое расположение точек, определяющих разностный шаблон и характер разностной аппроксимации производных: вперед, назад или центрально-разностная аппроксимация. Выбрав узлы (/- 1,/), (/,/) и (/+ 1,/),

3.4.2. Интерполяция функций полиномами

Интерполяция полиномами имеет много приложений в вычислительной гидродинамике и теплопередаче. Эту технику можно использовать для построения конечно-разностного аналога уравнений в частных производных, однако обычно ее применяют лишь для записи граничных условий или получения более подробной информации вблизи границ при известном численном решении задачи.

Рассмотрим несколько характерных примеров.

Пример 3.1. В этом примере мы построим конечно-разностные аналоги всех входящих в уравнение производных, предполагая, что решение этого уравнения локально аппроксимируется полиномом. Значения полинома в прилегающих к узлу (/, /) узлах разностной сетки должны совпадать с решением уравнения. Достаточное для точного определения коэффициентов полинома число узлов разностной сетки определяется степенью полинома. Продифференцировав интерполяционный полином, можно найти требуемую аппроксимацию входящих в уравнение производных. Рассмотрим уравнение Лапласа, описывающее стационарное двумерное распределение температуры в твердом теле:

d + -W~

Предположим, что в окрестности узла (г,/) зависимость температуры от X и у описывается полиномами второго порядка. Например, зафиксировав у, будем считать, что изменение температуры по X вблизи узла (/, /) описывается полиномом

Т(х, Уо) = а + Ьх + сх\

Для удобства положим, что а: = 0 в точке (/,/), а Ал: = const. Очевидно,