аппроксимации производной dT/dx\ii с помощью рядов Тейлора.

Сравнивая метод контрольного объема и метод построения разностных схем, основанный на разложении решения в ряд Тейлора, можно заметить, что последний позволяет построить конечно-разностную аппроксимацию всех входящих в дифференциальное уравнение производных путем суммирования конечно-разностных аналогов входящих в него производных. В противоположность ему метод контрольного объема, основанный на применении физических законов сохранения, дает возможность построить лишь конечно-разностный аналог всего уравнения в частных производных, однако в принципе с его помощью нельзя построить конечно-разностный аналог какой-то отдельно взятой производной, например производной ди/дх. Отличительной особенностью метода контрольного объема является то, что он обеспечивает «баланс» физической величины в окрестности узла разностной сетки. Метод контрольных объемов учитывает дискретный характер решения поставленной задачи, поэтому он обеспечивает выполнение законов сохранения в конечной области, а не только в точке при стремлении шага сетки к нулю. Конечно-разностные схемы, построенные методом контрольных объемов, почти всегда консервативны.

Трудно понять, чем могут отличаться разностные схемы, построенные для уравнения в частных производных всеми четырьмя указанными в этой главе методами, не рассмотрев большое количество примеров. Часто, особенно для линейных уравнений в частных производных, при использовании различных методов получаются одни и те же разностные схемы. Ни один из рассмотренных методов не гарантирует устойчивости построенной разностной схемы, поэтому построенная любым из этих методов разностная схема может оказаться бесполезной. Наиболее заметно отличие построенных различными методами разностных схем при использовании неортогональных систем координат и при аппроксимации записанных в недивергентной форме уравнений.

§ 3.5. Применение нерегулярных сеток

Наиболее удобными для проведения расчетов являются регулярные сетки с постоянными шагами Ах, Ау во всей расчетной области. Однако на практике такие сетки часто использовать не удается либо из-за того, что граница расчетной области не совпадает с узлами регулярной сетки, либо из-за необходимости сгущать сетку в некоторых подобластях для достижения требуемой точности решения задачи. При решении физических про-

блем нерегулярные сетки приходится использовать довольно часто, поэтому в вычислительной гидродинамике и теплообмене их применению уделяется довольно большое внимание. На практике, прежде чем вводить нерегулярную сетку, имеет смысл попробовать применить преобразование координат, позволяющее согласовать форму границы и регулярную сетку. Подробно различные преобразования координат будут рассмотрены в § 5.6.

3.5.1. Нерегулярные сетки, вводимые из-за формы границы области

В качестве примера рассмотрим случай, когда для решения задачи построена регулярная сетка с квадратными ячейками, т. е. Ах = Аг/ = const, но одна из границ расчетной области криволинейна. Вследствие этого расстояние от внутреннего узла сетки до границы непостоянно и отлично от шага сетки (рис. 3.8). Пусть мы хотим решить уравнение Лапласа при заданном на границе области значении искомой функции и. Для этой задачи ввести нерегулярную сетку можно несколькими различными методами, выписанными ниже.

1. Используем вблизи границы очень мелкую равномерную сетку, перенося граничное условие в узел сетки, ближайший к границе. Если вдали от границы не использовать более грубую сетку (при этом она оказывается нерегулярной на границе подобластей с мелкой и грубой сетками), то для достижения приемлемой точности необходимо провести расчет на сетке с очень большим числом узлов.

2. Используем линейную интерполяцию для определения значения функции и в каждом узле разностной сетки, отстоящем от границы области на расстояние, меньшее шага сетки. Интерполяция проводится по заданному значению функции и на границе области и ее значениям в узлах регулярной сетки, соседних с узлом, прилежащим к границе. Например, значение функции Up в точке Р на рис. 3.8 можно определить либо по формуле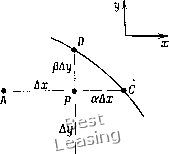

Рис. 3.8. Конечно-разностная сетка вблизи нерегулярной границы.

Hjl-

iJ+1

пределы интегрирования отстоящими на полшага сетки от этой точки. Тогда в соответствии с приведенными на рис. 3.9 обо-•ц. j значениями получим

Уо-У./2\х,-Ах /2 )

x\rx2

Рис. 3.9. Обозначения, использу- х-Ах /2 емые при решении уравнений на нерегулярной сетке.

dy\dx = 0.

(3.97)

Внутренние интегралы могут быть вычислены аналитически:

У-ЬАу,/2

Уо-Ау /2 х + Ах/2

х-Ах /2

I дх ди

Остальные интегралы можно вычислить, используя теорему о среднем значении:

. дх +

[хо + Уо) - 17 i,o--Уо)\-2-+

{ , ДУ+ ди ( АУ + А* (0, Уо + - 17 Уо - -JJ -= 0.

(3.98)

ди 1ду

либо по формуле

Можно использовать и среднее арифметическое этих двух значений: Up = {Up-]rUp)l2,

3. Построим конечно-разностную схему, пригодную для решения уравнения в частных производных на нерегулярной сетке.

Последнее проще всего сделать, используя интегральный метод на неравномерной сетке. Проинтегрируем дифференциальное уравнение в окрестности точки (хо,г/о), выбрав верхние и нижние