dt дх dv 1 ди г>

dt " Зх:

В рассматриваемом случае

. V .

Перепишем систему в матричном виде где

ГО с1

= 0.-

Следовательно, максимальное собственное значение матрицы [А] равно с и конечно-разностная схема устойчива при выполнении обычного условия устойчивости КФЛ

<1.

Отметим, что описанный выше метод анализа устойчивости конечно-разностных схем не учитывает влияния граничных условий, хотя и использует матричную запись системы уравнений в частных производных. Как учесть влияние граничных условий, будет показано ниже.

Соотношение (3.116) показывает, что устойчивость конечно-разностной схемы определяется видом матрицы перехода. Перепишем (3.116) в виде

е*+1(5) = [С(Д kritik)]. (3.120)

Теперь можно сформулировать условие устойчивости разностной схемы [Richtmyer, Morton, 1967]. Оно сводится к требованию существования такого положительного т, чтобы матрица [G(Atyk)] была равномерно ограничена при О < А/ < т, О nAt Т для любых А, где Т - максимальное время. Отсюда следует необходимое условие устойчивости Неймана:

I Oi (Д/, k) I <"1 + О (ДО при О < Д/ < т (3.121)

для всех собственных значений и волновых чисел, где а/ -собственные значения матрицы [0(Д/,)].

В рассмотренных примерах мы считали конечно-разностную схему устойчивой, если максимальное собственное значение

4 Д. Андерсон и др. Том 1

ных первого порядка

матрицы перехода по модулю не превосходит единицы. Это условие более сильное, чем (3.118). Необходимое условие устойчивости Неймана накладывает требование приемлемого роста локальной величины cAt, что в действительности возможно для решения многих физических задач. Классическим примером, иллюстрирующим это, является разностная схема решения уравнения теплопроводности с источниковым членом.

Пример 3.6. Пусть мы хотим решить уравнение теплопроводности с источниковым членом

ди дЧ ,

используя простую явную конечно-разностную схему. Применив анализ Фурье, найдем коэффициент перехода

G=l-4r sin2jp/2)-fcA/.

Отсюда следует, что решение данного разностного уравнения может расти по времени и удовлетворяет необходимому условию устойчивости Неймана. Мы видим, что при анализе устойчивости разностных схем полезно привлекать физические соображения. Следует помнить, что для системы гиперболических уравнений строгое условие заключается в том, что максимальное собственное значение не должно превосходить по модулю единицу. Это связано с тем, что гиперболические уравнения аналогичны волновому и не имеют экспоненциально растущих по времени решений.

Мы исследовали устойчивость различных конечно-разностных схем, используя метод Неймана. Если мы хотим изучить влияние граничных условий на устойчивость конечно-разностной схемы, то мы должны использовать матричный метод. Это проще всего показать на примере применения метода Лакса к решению одномерного линейного волнового уравнения первого порядка

dt дх ~

Пусть сетка по х состоит из т точек, а граничные условия периодические, т. е.

= (3.122)

Применяя для решения этой задачи метод Лакса, получим систему алгебраических уравнений вида

u+ = []u (3.123)

1-v

(3.124)

l±v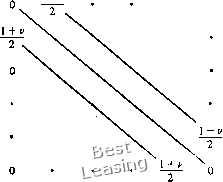

. (3.IZ5)

Устойчивость конечно-разностной схемы (3.123) зависит от собственных значений матрицы [X], Так как заданы периодические граничные условия, то в матрице [X] существенны лишь элементы на трех отмеченных в соотношении (3.125) диагоналях и два угловых элемента. Такая матрица называется апериодической [Lomax et al., 1970]. Для матрицы вида

02 О

(3-126)

собственные значения имеют вид

В рассматриваемом случае

Л/ = а, + (Оо + ог) cos - 1) + /(Оо - «г) sin (/ - О,