(а) (W (с)

Рис. 4.1. Влияние диссипации и дисперсии, (а) Точное решение. (Ь) Численное решение, полученное в том случае, когда ошибка является в основном диссипативной (такое решение типично для схем первого порядка точности), (с) Численное решение, полученное в случае, когда ошибка является в основном дисперсионной (такое решение типично для схем второго порядка точности).

ВВОДИТСЯ в разностное уравнение. Искусственная вязкость сглаживает решение уравнения, уменьшая градиенты всех параметров независимо от причины возникновения этих градиентов, физической или вычислительной. Такое свойство разностной схемы, обусловленное наличием в выражении для погрешности аппроксимации производных четного порядка, называют диссипацией на разностной сетке.

Другое близкое к физическому свойство разностных схем называют дисперсией. Оно непосредственно связано с производными нечетного порядка в выражении для погрешности аппроксимации. Дисперсия приводит к искажению соотношения фаз различных волн. Совместное воздействие диссипации и дисперсии на решение иногда называют диффузией. Диффузия приводит к растяжению крутых линий раздела, которые могут появляться в расчетной области. На рис. 4.1 показаны эффекты диссипации и дисперсии на расчет разрыва. Обычно если главный член в выражении для погрешности аппроксимации содержит производную четного порядка, то схема обладает в основном диссипативными свойствами, а если производную нечетного порядка- то дисперсионными,

ОН аналогичен диссипативному вязкому члену в одномерном уравнении движения жидкости. Например, если коэффициент вязкости 11 постоянен, то вязкий член в одномерном уравнении Навье -Стокса (см. гл. 5) можно записать в виде

-(т..) = 4-«... (4.16)

Следовательно, при v ф 1 схема с разностями против потока неявно вводит в уравнение искусственную вязкость, которую часто называют неявной (схемной) искусственной вязкостью в отличие от явной искусственной вязкости, которая преднамеренно

В ГЛ. 3 мы показали, как можно определить относительную погрешность в амплитуде (диссипацию) и фазе (дисперсию) каждой гармоники, зная коэффициент перехода. Поэтому естественно возникает вопрос: есть ли какая-либо связь между коэффициентом перехода и видом модифицированного уравнения. Оказывается, что такая связь действительно существует. Уор-минг и Хайет [Warming, Hyett, 1974] описали «эвристическую» теорию устойчивости разностных схем, основанную на анализе членов модифицированного уравнения с производными четного порядка, и определили погрешность, связанную с изменением

Единичная окружность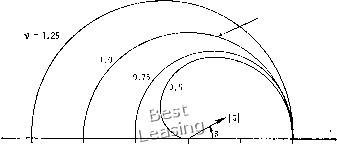

1.50

1.00

0.50

1,00

0.50 0.00

Рис. 4.2. Модуль коэффициента перехода для схемы с разностями против потока.

фазы, зная члены модифицированного уравнения с производными нечетного порядка. Прежде чем показать, как связан коэффициент перехода с видом модифицированного уравнения, запишем коэффициент перехода для рассматриваемой разностной схемы с разностями против потока в виде

G = (1 - V + V cos Р) - / (v sin Р). (4.17)

Его модуль

I G I = [(1 - V + V cos Р)2 -f (-V sin Р)2]/2

при различных v изображен на рис. 4.2. Из представленных на нем данных видно, что условие устойчивости Неймана G 1 выполняется лишь при v 1.

Загишем коэффициент перехода в виде G - \G\c\ где ф - фазовый угол, определяемый соотношением

, , Im(G) ,

-V sin р

1 - V + V cos р

Фазовый угол точного решения волнового уравнения фе определяется аналогично, если известен коэффициент перехода точного

решения волнового уравнения. Для определения точного значения коэффициента перехода подставим в волновое уравнение

его фундаментальное решение и - ее и найдем, что а = = -ikmC. Тогда u = etl и, следовательно, коэффициент перехода для точного решения имеет вид

Из последнего соотношения следует, что

где фе = -kmcAt = -pv, причсм I Gel = 1.

Итак, обусловленная диссипацией суммарная ошибка в определении амплитуды после п шагов решения волнового уравне-

Едипичнап окружность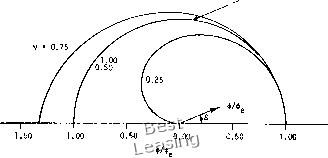

Рис. 4.3. Относительная погрешность определения фазы для схемы с разностями против потока.

ния по схеме с разностями против потока равна (1-С*)Ло, где Ло -начальное значение амплитуды волны. Аналогично полную дисперсионную ошибку (искажение фазы волны) можно записать в виде п(фе - ф)- Относительная погрешность в определении смещения по фазе на одном шаге по времени равна

Ф arctg [(-у sin Р)/(1 ~ у + у cos Р)] Фе -Pv

(4.18)

На рис. 4.3 показано отношение ф/фе при различных v. При малых волновых числах (т. е. если р мало) выражение для относительной погрешности в определении фазы можно привести к виду

JL:, (2v2 3v+I)PI

(4.19)