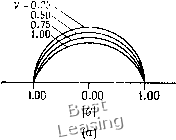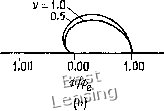Рис. 4.6. Неявный метод Эйлера, (а) Модуль коэффициента перехода; (Ь) относительная погрешность определения фазы.

диссипации при средних волновых числах и значительному запаздыванию по фазе при больших волновых числах.

4.1.5. Метод с перешагиванием (метод «чехарда»)

До сих пор мы в этой главе рассматривали лишь схемы первого порядка точности решения линейного волнового уравнения. В большинстве случаев эти схемы не используются для решения уравнений в частных производных из-за их низкой точности. Простейшим методом второго порядка точности является метод с перешагиванием. Применяя его к волновому уравнению первого порядка, получаем явную одношаговую трехслойную по времени разностную схему

Метод с перешагиванием называют трехслойным по времени, так как для определения значения и т (ai+ 1)-м шаге по времени необходимо знать значения и на {п- 1)-м и п-м шагах по времени. Метод имеет погрешность аппроксимации 0({Af)2, (Ал:)2) и устойчив при vl. Модифицированное уравнение имеет вид

щ + = (v - 1)- (9v - lOv+l) w+....

(4.38)

и относительная погрешность в определении фазы

Ф arc tg (- у sin Р) щ

Фе - Pv

построены на рис. 4.6. Неявный метод Эйлера ведет к сильной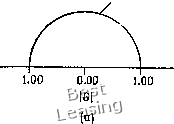

1.00

1.00

0.00

Рис. 4.7. Схема «чехарда», (а) Модуль коэффициента перехода; (Ь) относительная погрешность определения фазы.

(4.40)

или от округления, не затухают (предполагается, что граничные условия периодические, а vI). Коэффициент перехода

G = dz (1 - v2 sin2 P) - /V sin p (4.39)

и относительная погрешность в определении фазы

Ф arctg[-vsinp/± (1 ~v»sin»P)/] Фе -Pv

построены на рис. 4.7.

Хотя метод с перешагиванием имеет второй порядок точности и не вносит в решение диссипацию, он обладает рядом недостатков. Прежде всего начальные условия необходимо задать на двух временных слоях. С этой проблемой можно справиться, используя двухслойную схему на первом шаге по времени. Второй недостаток метода связан именно с «перешагиванием» (т. е. с тем, что не зависит от ufj, которое приводит к появлению при расчете двух независимых решений. И наконец, метод с перешагиванием предъявляет более высокие требования к памяти ЭВМ, так как является трехслойным по времени. Необходимую для расчета память ЭВМ можно существенно сократить, если вместо величины и"} записать величину ujK

Главный член в выражении для погрешности аппроксимации пропорционален производной нечетного порядка Uxxx, поэтому разностная схема должна обладать в основном дисперсионными свойствами. Последнее вообще характерно для схем второго порядка точности. Схему с перешагиванием отличает то, что в правой части модифицированного уравнения вообще нет производных четного порядка, поэтому связанные с диссипацией ошибки вообще отсутствуют. Следовательно, метод с перешагиванием нейтрально устойчив и любые появляющиеся при расчете ошибки, например ошибки от неточного задания граничных условий

1.00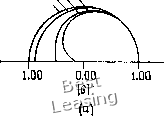

0.75 1.00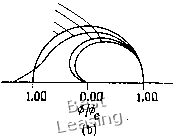

Рис. 4.8. Схема Лакса - Вендроффа. (а) Модуль коэффициента перехода; (Ь) относительная погрешность определения фазы.

грешностью аппроксимации О {(Ах) 2, (А/) 2), устойчивая при v 1. Модифицированное уравнение в этом случае имеет вид

«, + c«, = -«-(l-v2)«,,,--v(l-v2)«,,,,+ ....

(4.45)

Коэффициент перехода

G=l ~ v2(l-cosp)~ivsinP (4.46)

и относительная погрешность в определении фазы 0 „ arc {-- V sin - vl cos P)] }

4.1.6. Метод Лакса - Вендроффа

Схему Лакса - Вендроффа [Lax, Wendroff, 1960] можно пс-строить, исходя из разложения в ряд Тейлора:

ип = и- + Ш, + 72 (А0« + О т% (4.41)

Из волнового уравнения следует

щ = - cux, Utt = cxx- (4.42) Перепишем уравнение (4.41) в виде

= ис + 722 {Mf и + О mf) (4.43)

и заменим производные Ux и uxxy используя центральные разности второго порядка. В результате получим широко известную схему Лакса -Вендроффа

«г*=«" - Иг(«/%. -«/-.)+iw - 2"/+«/-•) • (-

Это явная одношаговая схема второго порядка точности с по-