«+1 =и--с {и-, - U-). (4.50)

изображены на рис. 4.8. Для схемы Лакса - Вендроффа характерно запаздывание по фазе, исключение составляют лишь гармоники с большими волновыми числами при л/о.5 < v < 1.

4.1.7. Двухшаговый метод Лакса - Вендроффа

Для решения нелинейных уравнений, например уравнений, описывающих движение невязкой жидкости, можно использовать двухшаговый вариант метода Лакса - Вендроффа. Применяя этот метод для решения волнового уравнения, получаем явную двухшаговую трехслойную по времени разностную схему:

Шаг 1

Шаг 2

,,«+1 „п ,,п+\/2 „ге+1/2

JV =: ,"/../2-«/-./30 (4.49)

Эта схема имеет второй порядок точности с погрешностью аппроксимации 0{{Ах) (ДО) и устойчива при v. 1. Шаг 1 - это просто метод Лакса, использованный для построения разностного уравнения в точке /+ 1/2 на полушаге по времени, а шаг 2 -метод с перешагиванием, примененный на оставшемся полушаге по времени. В случае линейного волнового уравнения первого порядка двухшаговый метод Лакса - Вендроффа эквивалентен описанному в предыдущем разделе методу Лакса - Вендроффа. В этом легко убедиться при помощи подстановки (4.48) в (4.49). Так как оба метода эквивалентны, то и модифицированное уравнение, и коэффициент перехода у них будут одинаковы.

4.1.8. Метод Мак-Кормака

Метод Мак-Кормака [МасСогтаск, 1969] широко применяется для решения уравнений газовой динамики. Фактически это один из вариантов двухшагового метода Лакса - Вендроффа, не требующий вычисления значений искомой функции в точках /+1/2 и /-1/2. Благодаря этому метод Мак-Кормака особенно удобен для решения нелинейных уравнений в частных производных, как это будет показано в п. 4.4.3. Применяя явный метод предиктор-корректор к линейному волновому уравнению, получаем следующую разностную схему:

Предиктор

Корректор

,у«+1 = J-

Первоначально (предиктор) находится оценка и- величины W на (Az-f 1)-м шаге по времени, а тююм (корректор) определяется окончательное значение и нл (n + l)" шаге по времени. Отметим, что в предикторе проигодная ди/дх аппроксимируется разностями вперед, а в корректоре - разностями назад. Можно поступить и наоборот, что бывает полезным при решении некоторых задач. К таким задачам относятся, в частности, задачи с движушимися разрывами. Для линейного волнового уравнения схема Мак-Кормака эквивалентна схеме Лакса- Вендроффа, поэтому у них одинаковые погрешность аппроксимации, условие устойчивости, модифицированное уравнение и коэффициент перехода.

4.1.9. Разности против потока

Бим и Уорминг [Warming, Beam, 1975] предложили несколько изменить метод Мак-Кормака, используя как на шаге предиктор, так и на шаге корректор разности назад (разности против потока). При с Г> О этот метод приводит к разностной схеме.

Предиктор

"Г к-«/-.)• (4.52)

Корректор

«/+«Г--(«Г-«/-)-

-К-2"?-1 + «?-2)]- (4.53)

Благодаря тому чго в правую часть уравнения (4.53) включена односторонняя с разностями против потока аппроксимация второй производной, схема имеет второй порядок точности с погрешностью аппроксимации 0((Дг) (Д (Ал:), (Ал:)2). Если подставить (4.52) в (4.53), то получится одношаговый алгоритм

= uv{u- и) f 1V (V - - 1) {и - 2и + и ). (4.54)

При V = 1 и V = 2 схема с разностями против потока имеет бесконечный порядок точности. Коэффициент перехода выражается в виде

0=1 -2v

v-f 2(1 -V) sin2 I

-/vsinp 1+2(1-v)sin2-

sin P

(4.56)

и разностная схема устойчива при О v 2. Модуль коэффициента перехода и относительная погрешность в определении фазы показаны на рис. 4.9. Для метода с разностями против

J/=1.25, 0.75.

2.00, 1.00

1.50, 0.50

1.75, 0;-

0.59-0Л5~ 1.00 1.25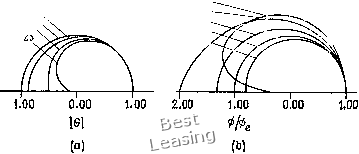

Рис. 4.9. Схема с разностями против потока (Бима - Уорминга). (а) Модуль коэффициента перехода; (Ь) относительная погрешность определения фазы.

потока при О < V < 1 характерно в основном опережение по фазе, а при 1 < v < 2 - отставание. Отметим, что при О < v < < 1 метод Лакса - Вендроффа и метод Бима и Уорминга с разностями против потока имеют противоположные ошибки по фазе, поэтому дисперсионную ошибку можно существенно уменьшить, применив линейную комбинацию двух этих методов. Метод Фромма [Fromm, 1968] с равной нулю средней ошибкой по фазе основан именно на этой идее.

Модифицированное уравнение для рассматриваемой разностной схемы имеет вид

Щ + си, = (1 V) (2 - V)-

-(-П2-У)и,,,,+ .... (4.55)