Модуль коэффициента перехода и относительная погрешность в определении фазы приведены на рис. 4.11. Из рисунка видно,

17=1.00,(=3,0

3/0.75, о; =2.5

]/=0.50, w=1.5 1/=1.00,б;=3.0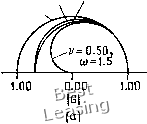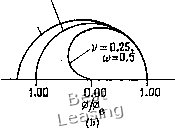

Рис. 4.11. Схема Русанова, (а) Модуль коэффициента перехода; (Ь) относительная погрешность определения фазы.

ЧТО При использовании метода Русанова опережение или запаздывание по фазе определяется величиной параметра (о.

4.1.12. Метод Уорминга - Катлера - Ломакса

Уорминг и др. [Warming et al., 1973] предложили метод третьего порядка точности, который на первых двух шагах по времени совпадает с методом Мак-Кормака и на третьем - с методом Русанова:

Шаг 1

Шаг 2

Шаг 3

**/ 2

- Т V - - 4«, + 6«7 - 4«7 , + ииУ (4.70)

Условия устойчивости рассматриваемого метода такие же, как и метода Русанова. Кроме того, в случае волнового уравнения первого порядка и модифицированное уравнение совпадает с (4.66). Метод Уорминга -Катлера -Ломакса обладает перед методом Русанова теми же преимуществами, что и метод Мак-Кормака перед двухшаговым методом Лакса - Вендроффа.

При использовании методов третьего порядка точности за увеличение точности алгоритма приходится расплачиваться увеличением времени счета и усложнением разностной схемы. Это необходимо тщательно учитывать при выборе метода решения уравнения в частных производных. Обычно для большинства приложений достаточную точность позволяют получить методы второго порядка точности.

При решении одномерного линейного волнового уравнения первого порядка явные методы второго порядка точности, например методы Лакса - Вендроффа или Бима - Уорминга, дают прекрасные результаты с минимальными вычислительными усилиями. Неявные методы для решения этого уравнения использовать нецелесообразно, так как решение нестационарно, и нас обычно интересуют значения величин через небольшие промежутки времени.

§ 4.2. Уравнение теплопроводности

Одномерное уравнение теплопроводности (уравнение диффузии)

ди ди

1Г = «ЖГ (4.71)

является параболическим уравнением в частных производных. Оно описывает одномерный процесс распространения тепла или одномерную диффузию в однородной изотропной среде. Это уравнение является простейшим модельным уравнением для параболических уравнений. Точное решение уравнения теплопроводности с начальным условием г(л:, 0)= /(х) и граничными условиями i(0, 0 = «(1» 0 = 0 имеет вид

и (а:, t)=Yu Ае- sin (kx), (4.72)

An = 2f{x) sin (kx) dXy k = nn,

Перейдем теперь к изучению некоторых наиболее важных разностных схем решения уравнения теплопроводности.

4.2.1. Простой явный метод

Явный одношаговый метод

-Д?--°-- (4-73)

имеет первый порядок точности с погрешностью аппроксимации

О (At, (Аде) 2). В стационарном случае погрешность аппроксимации равна О ((Ал:) 2). Как показано выше, такая разностная схема устойчива при

0<г<72, (4.74)

r = aM/{Axf. (4.75)

Модифицированное уравнение в рассматриваемом случае имеет вид

1 .9 л. . а(Ах)-

Uxxxx +

а(АхУ

+ .... (4.76)

Отметим, что при г =1/6 погрешность аппроксимации равна 0((А/) (Ах)). Интересно также заметить, что в выражение

1.00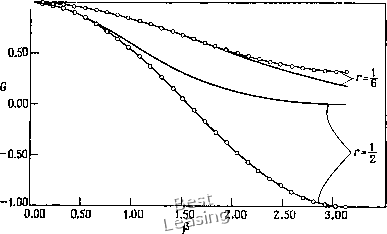

Рис. 4.12. Коэффициент перехода для простой явной схемы. -о- простой явный метод;- точное решение.

ДЛЯ погрешности аппроксимации не входят производные нечетного порядка. Поэтому для этого метода, так же как для большинства других методов решения уравнения теплопроводности, дисперсия на разностной сетке отсутствует. Этот факт следует и из анализа выражения для коэффициента перехода рассматриваемой схемы:

G=l + 2r(cosp-l), (4.77)

причем мнимая часть этого коэффициента перехода равна нулю и, следовательно, сдвиг по фазе отсутствует. На рис. 4.12 про-