мая задача похожа на задачу о распространении центрированной волны разрежения в течении сжимаемой жидкости. В случае уравнения Бюргерса волна разрежения ограничена слева линией л: = О, а справа - проходящей через начало координат характеристикой, которая изображена на рисунке штриховой ли-

Рис. 4.25. Начальные условия дли волны разрежения.

иней. Математически решение задачи о распространении волны разрежения можно записать в виде

м = 0, а:<0,

u = x/t, 0<x<i,

u=l xt.

Итак, заданное начальное распределение и приводит к образованию центрированной волны разрежения, ширина которой растет по времени линейно.

Мы изучили две задачи, часто встречающиеся в сверхзвуковых газодинамических течениях-ударные волны и волны разрежения, - которые можно моделировать при помощи уравнения Бюргерса. Решения такого типа существуют и для других нелинейных гиперболических уравнений в ча-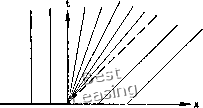

Рис. 4.26. Характеристики для случая центрированной волны разрежения.

стных производных. Вооружившись простыми аналитическими решениями для двух этих важных случаев, перейдем к изучению различных разностных схем решения невязкого уравнения Бюргерса.

4.4.1. Метод Лакса

Схемы первого порядка точности почти не используются для решения гиперболических уравнений в частных производных. Метод Лакса [Lax, 1954] выбран как типичный метод первого

dt дх

Применим метод Лакса. Для этого выпишем первые два члена ряда Тейлора для функции и в точке (х, t):

и{х, t + At) = u{x, +

При помощи исходного уравнения заменим производную по времени; тогда запишем

и{х, t + At) = u{x, )д() д ....

Следуя методу Лакса, для аппроксимации производной используем центральные разности, а первое слагаемое в правой части представим как среднее арифметическое значение в двух соседних узлах (см. п. 4,1.3). В результате получим

»„.."ж + "/- 1ж;/-.. (4.139)

Для уравнения Бюргерса F=u/2. Коэффициент перехода в этом случае запишется в виде

G = cos р - / Л sin р, (4.140)

где якобиан А = df/du для уравнения Бюргерса равен просто и. Условие устойчивости схемы Лакса имеет вид

<1, (4Л41)

так как итгх - максимальное собственное значение матрицы Л, состоящей лишь из одного элемента и.

Результаты расчета методом Лакса движущегося вправо разрыва 1-0 приведены на рис. 4.27. Положение движущегося разрыва определяется довольно точно, однако диссипативные свойства метода проявляются в размазывании разрыва на несколько шагов разностной сетки. Как уже отмечалось раньше, это размазывание должно быть тем больше, чем меньше число Куранта. Интересно заметить, что при расчете разрывных ре-

порядка точности для того, чтобы показать, что такие методы позволяют решать нелинейные уравнения, но обладают сильными диссипативными свойствами.

Для построения разностной схемы, как и при построении всех последующих примеров, воспользуемся дивергентной формой записи исходного уравнения

"+ = 0.

шений метод Лакса приводит к одинаковым значениям и в двух соседних узлах, как показано на рисунке. Укажем еще на одно свойство метода Лакса - его монотонность, т. е. на отсутствие осцилляции решения. С. К. Годунов [1959] показал, что схемы с более высоким, чем первый, порядком точности не могут быть монотонными Если расчет разрыва является лишь частью более общей задачи, то желательно проводить его, используя мо-

и = 1 ~о-:го=югс>-я- ---jQg решение

-о- At/Дх = 0.6 -СН At/Ax = 1.0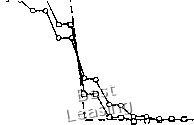

Рис. 4.27. Результаты численного решения уравнения Бюргерса по схеме Лакса.

нотонную схему, однако диссипативные свойства методов первого порядка точности велики, поэтому вопрос о целесообразности использования монотонной схемы необходимо решать в каждом конкретном случае.

4.4.2. Метод Лакса - Вендроффа

Метод Лакса -Вендроффа [Lax, Wendroff, I960] -один из первых конечно-разностных методов второго порядка точности, созданных для решения гиперболических уравнений в частных производных. Для нелинейных уравнений разностную схему можно построить, исходя из разложения в ряд Тейлора:

„(../+ад=«(«,о+д/(--),.,+4(11,+ --

Первую производную по времени можно заменить при помощи исходного уравнения в частных производных. Сложнее обстоит дело со второй производной. Запишем исходное уравнение в виде

ди дР

> Все результаты были получены С. К. Годуновым лишь для так называемых однородных разностных схем. В последние годы создан ряд неоднородных монотонных разностных схем высокого порядка точности для решения гиперболических уравнений. Они описаны, например, в работах [2, 3, 11, 15, 27, 31] в списке дополнительной литературы на стр. 7\2. - Прим. перев.