ТО при проведении расчета параметр 0 может меняться от точки к точке, а законы сохранения на разностной сетке будут выполняться. При таком подходе член, содержащий 0 в соотношениях для последнего шага схем Русанова и Уорминга - Катлера -Ломакса, запишется в виде

- т («/\2 - з«/%. + Щ - «?-,) +

+ К+. - 3«? + Зи; . - (4-149)

Величины cDj2 зависят теперь от эффективного сеточного числа Куранта. Уорминг и др. [Warming et al., 1973] предложили в каждом узле выбирать эти параметры так, чтобы свести к минимуму либо дисперсионную, либо диссипативную ошибку.

Модифицированное уравнение для схем третьего порядка точности проанализировано в п. 4.1.11. Если мы хотим минимизировать дисперсионную ошибку, то в соответствии с (4.68) должны задать параметр по формуле

Теперь осталось лишь разумно определить эффективное число Куранта Vf±i{2. Уорминг и др. [Warming et al., 1973] предложили при определении коэффициентов ©/ ± 1/2 полагать эффективное число Куранта равным среднему значению чисел Куранта в узлах сетки, используемых для разностной аппроксимации соответствующего члена. Так как член с 0/+1/2 содержит значение неизвестной в узлах / + 2, /+ 1, / и /-I, то можно записать

v/+,/2 = J (Я;2 + h-l + h + /-1) XT (" 15)

и аналогично

v/-1/2 = j (Я/ + 1 + Я/ + + Я/ 2) ,

где Я, -локальное собственное значение. Для уравнения Бюргерса X просто совпадает с неизвестной и. Результаты расчетов с переменным 0 (расчетов по самонастраивающейся схеме) приведены на рис. 4.34. Из рисунка видно, что оба метода третьего порядка точности позволяют получить удовлетворительные результаты, если разностная схема строится из соображений минимальной дисперсии. Слева от разрыва наблюдается неболь-

u = 1 -u-v4--ti ---Точное решение

Русанова Т v = 0.6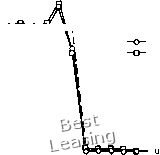

Рис. 4.34. Решение уравнения Бюргерса, полученное самонастраивающимся методом (методом с переменным со).

«/±1/2 может быть вычислен различными способами, но он должен быть выбран так, чтобы не изменилось условие устойчивости разностной схемы. Очевидно, при разных методах определения этого параметра будут получаться различные численные решения.

4.4.7 Неявные методы

Центрированный по времени неявный метод описан в п. 4.1.10. Его основу составляют соотношения (4.57). Подставляя в (4.58) производные по времени из рассматриваемого нами модельного уравнения, получаем

"r="?-f[(lf)"+(fr]. (4.152)

Задача оказывается нелинейной, и для ее решения необходимо применить линеаризацию или итерационный метод. Бим и Уорминг [Beam, Warming, 1976] предложили воспользоваться следующим приближенным соотношением:

f - Г + ("- и"") = F+A (и"" - и%

шое превышение точного решения, справа же решение почти совпадает с точным. Мы не советуем определять параметр (0/±i/2 из соображений минимума диссипации. Член, содержащий параметр 0, добавлен в уравнения для стабилизации решения, поэтому при уменьшении диссипации могут возникнуть проблемы с устойчивостью разностной схемы. Сильные осцилляции могут появляться даже в устойчивом решении. Отметим, что параметр

186 Гл. 4. Метод конечных разностей для модельных уравнений Тогда

ur=uf- {2 + [Л - ««)]}.

Используя центральные разности для аппроксимации производных по X со вторым порядком точности, получаем

4Длг "/-1+"/ + 4Д* "/+1- Д7 2

+ + (4.153)

В случае уравнения Бюргерса матрица Якоби А состоит лишь из одного элемента, и поэтому правую часть можно упростить. Мы видим, что предложенная линеаризация Бима и Уорминга позволяет получить на новом временном слое систему линейных алгебраических уравнений. Это система уравнений с трехдиагональной матрицей, которая легко может быть решена прогонкой.

В п. 4.1.10 было показано, что рассматриваемый метод устойчив при любых шагах по времени. Следует заметить, что все корни характеристического уравнения лежат на единичной окружности, что согласуется с отсутствием в модифицированном уравнении членов с производными четного порядка. Вследствие этого в схему приходится вводить искусственную диссипацию. Можно, например, к уравнению (4.153) добавить член, пропорциональный разностной производной четвертого порядка

- Т («/"+2 - 4и?+, + б«? - 4«« , + u1 ,), (4.154)

не изменив формального порядка аппроксимации разностной схемы. Согласно Биму и Уормингу, неявная разностная схема (4.153) с явным демпфирующим членом устойчива при

0<а)<1. (4.155)

Результаты расчета движущегося вправо разрыва по центрированной по времени неявной разностной схеме показаны на рис. 4.35. Очевидно, что решение, полученное по схеме без демпфирования, неприемлемо. При введении в разностную схему демпфирующего члена по формуле (4.154) получаются существенно лучшие результаты.

Кроме только что описанного метода, Бим и Уорминг [Beam, Warming, 1976] предложили еще два аналогичных метода - неявный метод с трехточечной аппроксимацией производных назад и неявный метод Эйлера. Вариант неявного метода Эйлера, предложенный Бимом и Уормингом, основан на методе Эйлера