§ 4.4. Уравнение Бюргерса (невязкое течение) С разностями назад

и- = и- + М (If)".

Для рассматриваемого нами нелинейного уравнения последнее соотношение примет вид

Применяя уже описанную линеаризацию, получаем

2hx "/-1"/ + 2Дх "/+1 "~ Дл; 2

£Л1 /ул 4 /уп I /- 1,п

(4.156)

Задача снова свелась к легко решаемой системе линейных алгебраических уравнений с трехдиагональной матрицей. Полу-

U = 1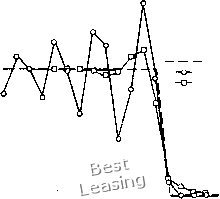

Точное решение без демпфирования с демпсрированигм

V = 0.5

03 = 0.5

20 шагов

г) = о

Рис. 4.35. Решение уравнения Бюргерса, полученное цептрировашюй по времени неявной схемой Бима - Уорминга.

чившаяся разностная схема безусловно устойчива, но для получения приемлемых численных результатов в нес необходимо ввести демпфирующий член, например по формуле (4.154).

Более простой вид описанных в этом разделе неявных разностных схем получается, если их записать в так называемой дЫьта-форме, т. е. в тех случаях, когда разностные уравнения составляются для приращений величин и для потоков, входящих в законы сохранения. Преимуществом такой записи разностных схем при решении многомерных задач является то, что

стационарное решение, если оно существует, не зависит от шага по времени. Построим центрированную по времени неявную разностную схему, используя дельта-форму записи разностных уравнений. Пусть Аи. = и- - uj. Тогда уравнение (4.152) можно переписать в виде

Проведя, как и раньше, локальную линеаризацию, получим

Fr = F} + AlMj, Окончательно разностное уравнение запишется в виде

--4Г"/-1 + Д"/ ТЁ

(4.157)

Оно имеет более простой вид, чем уравнение (4.153). Система линейных алгебраических уравнений осталась трехдиагональ-

U = 1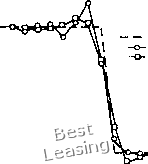

- Точное решение без де;п(рирования с демпд}ироваиием

V = 1.0 ш = 1.0

Рис. 4.36. Решение задачи о движущемся вправо разрыве, полученное центрированной по времени неявной схемой, записанной в дельта-форме.

НОЙ, НО ЧИСЛО членов в правых частях уменьшилось. Связанное с этим сокращение объема вычислений может оказаться особенно существенным при решении систем уравнений, когда объем вычислений очень большой. Решив уравнение (4.157) найдем приращения неизвестных на одном шаге по времени Как уже отмечалось, записанная в дельта-форме схема без условно устойчива, но и к ней необходимо добавить демпфи рующие члены более высокого порядка. На рис. 4.36 представ лены результаты расчета движущегося вправо разрыва по схеме использующей дельта-форму записи. Как и следовало ожидать решения с демпфированием и без демпфирования идентичны ре-

является параболическим уравнением в частных производных. Оно используется как модельное для уравнений пограничного слоя, «параболизованных» уравнений Навье -Стокса и полных уравнений Навье - Стокса. Для лучшего моделирования уравнений пограничного слоя и параболизованных уравнений Навье - Стокса независимые переменные и л: можно заменить независимыми переменными хну; тогда получим

ди , ди ди /. .rCi\

где х -маршевая координата.

Как и в случае ранее рассмотренных модельных уравнений, для уравнения Бюргерса существуют точные аналитические решения при некоторых начальных и граничных условиях. Эти решения полезно использовать для сравнения различных разностных схем. Точное стационарное решение [т. е. lim и{х, /)]

уравнения (4.158) с граничными условиями

(0, t)=u,, (4.160)

u{L, 0 = 0 (4.161)

шениям, полученным при развернутой записи разностных уравнений. При применении центрированной по вре.мени схемы мы рекомендуем использовать дельта-форму, а не развернутую запись разностных уравнений. Если ищется асимптотическое по времени решение, то члены, содержащие Аи, стремятся к нулю и, кроме того, во всех случаях необходимо вычислять меньше матричных произведений.

Рассчитанные по неявным разностным схемам решения невязкого уравнения Бюргерса обычно хуже рассчитанных по явным схемам; при этом на каждом шаге приходится производить больший объем вычислений. Кроме того, часто надо знать промежуточные результаты, поэтому возможность использовать больший шаг по времени в случае неявной схемы обычно особой роли не играет. При расчете разрывных решений явные схемы позволяют получить лучшие результаты, чем неявные схемы, использующие центральные разности; поэтому мы рекомендуем для решения уравнения Бюргерса для невязкого течения применять явные методы, например метод Мак-Кормака.

§ 4.5. Уравнение Бюргерса (вязкое течение)

Полное нелинейное уравнение Бюргерса