Следовательно, условие устойчивости (4.177) можно записать в виде

ReAx<2/v. (4.179)

Мы уже отмечали раньше, что эвристический анализ устойчивости не всегда позволяет определить все условия устойчивости разностной схемы. В рассматриваемом нами сейчас случае так и произошло. Чтобы получить все условия устойчивости, воспользуемся фурье-анализом (методом Неймана). Для схемы ВВЦП коэффициент перехода

G = 1 + 2г (cos Р - 1) ~ /V (sin Р) (4.180)

построен на рис. 4.38(a) для данных v и г. Уравнение для G описывает эллипс с центром в точке (1 -2г) вещественной оси.

Единичная ..........

окружность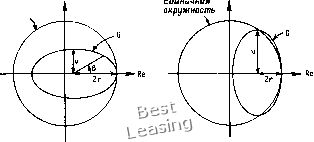

Рис; 4.38. Условие устойчивости схемы ВВЦП. (а) v < 1, г < 1/2, < 2г; (Ь) v < 1, г < 1/2, v2 > 2г.

Большая и меньшая полуоси эллипса равны 2г и v соответственно. Кроме того, эллипс касается единичной окружности в точке пересечения этой окружности с положительной вещественной осью. Необходимое условие устойчивости G 1 эквивалентно требованию, что эллипс целиком содержится внутри единичной окружности. Последнее условие накладывает следующие ограничения на длины большой и малой полуосей эллипса:

v<l, 2г<1. (4.181)

Однако и при выполнении этих условий разностная схема может быть неустойчива, как видно из рис. 4.38(b). Конечно, полное условие устойчивости можно найти, исследуя обычным образом выражение для модуля коэффициента перехода. Проведя такой анализ, получим

v2<2r, г<1/2. (4.182)

Первое условие уже было получено раньше на основе эвристического анализа устойчивости. Комбинируя эти два неравенства, можно определить еще одно: v 1, которое уже было получено на основе графического анализа. Условия устойчивости накладывают следующие ограничения на величину сеточного числа Рейнольдса:

2v<ReAx<2/v. (4.183)

Следует заметить, что в некоторых работах правая часть последнего неравенства ошибочно записывается как Яех 2.

Важной характеристикой конечно-разностных схем, используемых для решения уравнения Бюргерса, является появление осцилляции (всплесков) решения. Очевидно, при расчете течений жидкости мы хотели бы избежать появления таких осцилляции. При решении уравнения Бюргерса методом ВВЦП осцилляции возникают, если сеточное число Рейнольдса расположено в диапазоне

2<ReAx<2/v.

Если сеточное число Рейнольдса немного больше 2/v, то эти осцилляции в конце концов приведут к «взрыву» решения, как и следовало ожидать из проведенного выше анализа устойчивости. Чтобы найти причину возникновения осцилляции, перепишем уравнение (4.175) в виде

u+i = (г - V/2) и-, + (l--2r)u- + {r + v/2) (4.184)

или, что эквивалентно, в виде

Г = Т(2 - RAx)+ (1 - 2г)+ I(2 + Reд,)ul,, (4.185)

Теперь предположим, что мы хотим найти решение уравнения Бюргерса с начальным условием w(a:, 0) = 0, О л: < 1, и граничными условиями м(0,/) = 0, u{lyt)==l на сетке, состоящей из 11 узлов. На первом шаге по времени все значения и на (д-f 1)-м временном слое равны нулю, кроме значений в узле / = 10, где

= I (2 - ЯвАх) (1) + (1 - 2г) (0) +1 (2 +ЯеАх) (0) = -=(2-ReA

и на границе (/=11), где иц равно заданному значению 1. Если Rcajc больше двух, то величина и будет отрицательна, что и вызовет осцилляции решения, как показано на рис. 4.39(a).

Этот рисунок построен для случая v = 0.4, г = 0.1, Яех - 4 < < 2/v. При этих параметрах wQ+* равно -0.1. На следующем шаге по времени осцилляция продвигается еще на одну точку дальше от правой границы. Значения и при / = 9 и / = 10 равны м+ = + 0.01, и5(+ = - 0.18, а вид решения показан на рис. 4.39(b). Постепенно осцилляции распространяются до другой границы, но при этом остаются ограниченными по величине

l.Or

0,9-

0.8-

0,7-

0.6-

0.5-

0.4-

0.3-

0.2 -

0.1 -

0.0 -

-ОЛ -

-0.2-

-0.3-1

3 5 7 9 11 J

3 5 7 9 Л

1 3

-J L

5 7 9 n

Рис. 4.39. Возникновение осцилляции при численном решении уравнения Бюргерса. (а) (л-f 1)-й слой по времени; (Ь) (n-f2)-ft слой по времени; (с) (/г + 3)-й слой по времени.

В течение всего решения, пока итерационно не получится стационарное состояние. Рассмотренные осцилляции аналогичны тем, которые возникают в рамках невязкого уравнения Бюр- герса при расчете движущегося разрыва по схемам второго (или более высокого) порядка точности.

Лучше понять причины возникновения осцилляции можно, также изучив коэффициенты уравнения (4.185) с физической точки зрения. Мы видим, что если Яех больше двух, то коэффициент при ufj становится отрицательным. Следовательно, чем больше и!}у, тем меньше иК Для вязких задач такое поведение решения не имеет физического смысла, так как с ростом iyj величина должна «тянуться» за ней все сильнее и