где Моо - число Маха, посчитанное по параметрам невозмущенного потока

и уравнение состояния совершенного газа (5.39) приводится к виду

p- = (V-l)pV, г=.

Заметим, что безразмерные уравнения (5.45) и (5.46) идентичны размерным уравнениям (5.43) и (5.44), сли в записи уравнений опустить звездочку. Для сокращения записи звездочки в безразмерных уравнениях можно опускать, что обычно и делают.

5.1.7. Криволинейные ортогональные координаты

Уравнения динамики жидкости могут быть записаны в любой системе координат. Ранее мы выписали эти уравнения для декартовой системы координат. Во многих приложениях удобнее пользоваться какой-либо другой ортогональной системой координат. Определим криволинейную ортогональную систему координат общего вида лгь Х2, л:з, начало которой находится в точке Р, и пусть ii, 12, 1з - соответствующие единичные векторы (рис. 5.2). Координаты декартовой прямоугольной системы связаны с криволинейными координатами общего вида соотношениями

X = x{xiy Х2у х)у

У = у{хи 2, з), (5.48)

Z = z{Xiy ЛГз, АГз).

Если якобиан д{х, у, г) /д{хиХ2, х) отличен от нуля, то

Xi = Xi {х, у, г),

Х2 = Х2{х, У, Z), (5.49)

x = xs{x, У, Z).

230 Гл. 5. Основные уравнения механики жидкости и теплообмен Длина элемента дуги в декартовых координатах равна {dsf=-idxf + {dijf + {dzf.

(5.50)

Если уравнения (5.48) продифференцировать и подставить в уравнение (5.50), то получим

{dsf = (Л, dxf + (Лг dxf + (Лз dxf, (5.51)

Пусть ф - произвольный скаляр, А - произвольный вектор, тогда для градиента, дивергенции, вихря и оператора Лапласа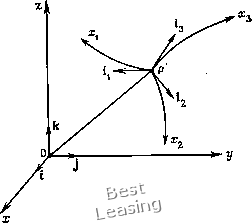

Рис. 5.2. Ортогональная криволинейная система координат.

в криволинейных координатах общего вида имеем следующие выражения:

1 дф . , \ дф. . 1 дФ.

hi dxi

hi dxt

hz dxz д

(5.52)

VXA-

i(M3)-(M2)]i.+

(M,)-ir(M3)]i.+ + Лз[-з(М2)-(лИ)]ь

--3 V Иг дкг )У

(5.54)

(5.55)

Выражение V-VV, входящее в член D\/Dt уравнения движения, можно представить в виде

hi dxi ~ hi дхз

-) (Uih + 422 + ИзЬ).

где Ml, «2, «3 - компоненты вектора V по направлениям xi,X2,Xz. Учитывая, что единичные векторы суть функции координат, цо-лучим

V-VV

4-

«, ди

, «3 а«, и,«2 сЛ

dXi hi dXi hi дхз hht дхг

ии dh

hihi дхъ ди

mjmg dh UcyU

/zi2 dxi hih дх

dh£\ dxi )

(5a: 1 Л2 <5x2 Лз дх

/ii/i2 hihz дх

Лг/гз дх2

h\h2 дх2

Ii2 +

"2 t"3

«3 ди

13 3

Лг/гз hihz дх

*2"3

23 <5а:;

Компоненты тензора напряжений (5.15) можно выразить через координаты х\, х, Хз следующим образом:

(5.56)