ex,X =

XzXi -

XiX2 -

1 dui hi dxi

1 dU2

h2 dX2 1

hz dxz

hi dx<

hx д

hz dxz

h2 д

U2 dhi

Л1Л2 dx2

Uz dh2

Л2Л3 dxz

Ul dhz

hxhz dxi

Uz dhi hihz dx2 и I dh2

h\h2 dx\ U2 dhz

hihz dx2

2\hz) hz dXz Khz) f tii\ hz д ( Uz\ К hi J hi dxiKhz)

hi dxi\h2 ) h2 dx2 \hi )

(5.57)

Компоненты V • П-у суть

+ г1

Х1Х2

1 dhi

hih2 dx2

1 diH

hihz dxi

1 dhi Л1Л3 дхз

1 (ЭЛ.

hihi dxi

1 dh2

1 алг

1 dhi

1 dhi

hih2hz + П

1 (5/i3

/г1/гз dxi

I 5/Z2

1 dhz

1 a/li Ai/l3 АГз

X-X2

h2hz dxz

В криволинейных координатах диссипативная функция принимает вид

(5.59)

где выражения для компонент тензора скоростей деформаций записываются в виде

т- , ,

для осесимметричного течения.

§ 5.2. Уравнения Рейнольдса для турбулентных течений 5.2.1. История вопроса

Более пятидесяти лет тому назад стало понятно, что наши знания о турбулентности далеки от полноты. Датированное 1932 годом высказывание Г. Ламба остается актуальным и поныне: «Я старый человек и, когда после смерти попаду на небеса, то спрошу у Всевышнего две вещи: что такое квантовая электродинамика и что такое турбулентность. В отношении пер-р.ого я настроен более оптимистически»;

Все выписанные выше формулы можно использовать для получения уравнений динамики жидкости в любой криволинейной ортогональной системе координат. Ниже приведено несколько таких примеров.

1. Декартовы координаты

Xi = x, /г, = 1, щ=и,

Х2 = У, 2=1, ti2=-v,

Xs = z, Аз=1, Us = w.

2. Цилиндрические координаты

Xi = r, Ai = l, щ = иг,

X2 = Qy h2 = r, U2 = Uq,

3. Сферические координаты

Х\ = г, Ai = l, Щ=иг,

X2 = Qy h2 = r, U2 = Uq,

Хг = фу h = rsmQy щ = иф.

4. Двумерные осесимметричные связанные с поверхностью тела координаты

Хх = 1. Ai = 1 + Л:()т1, 1 Щ = и,

Х2 = % h2=U tl2 = V,

Хг = Ф. Лз = [г (Ю + Л cos а {1)Г, щ = ш = О,

где/C(g) -локальная кривизна поверхности тела, г(g)--радиус цилиндра (рис. 5.3) и

О для двумерного течения,

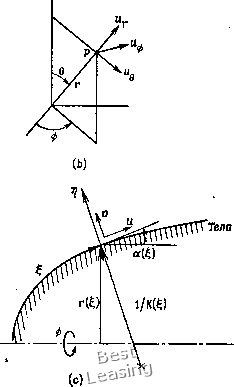Рис. 5.3. Криволинейные системы координат, (а) Цилиндрические координаты (г, 9, г); (Ь) сферические координаты (г, 9, Ф)\ (с) связанные с поверхностью тела координаты в двумерном или осесимметричном случае 0).