Исходные дифференциальные уравнения, записанные вдоль характеристик, называются уравнениями совместности. Их можно вывести, решая исходную систему уравнений для первых производных. Вдоль характеристических направлений определитель коэффициентов системы обращается в нуль. Если мы ищем решение для любой из первых производных, например для ди/дх, и требуем, чтобы они были по крайней мере ограниченными, то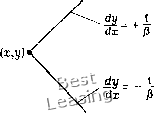

Рис. 6.1. Характеристики уравнения Прандтля - Глауэрта.

должен обращаться в нуль и определитель матрицы, образованной любыми четырьмя столбцами расширенной матрицы. Это может быть записано в виде

= 0.

(6.10)

Раскрывая этот определитель, получаем уравнения совместности

ds ~"\dx ) ds

ifm + v) = 0

(6.11)

вдоль распространяющейся вправо характеристики dy/dx =

= -1/М

im-v)=o (6.12)

вдоль распространяющейся влево характеристики dy/dx = 1/р.

Более общая процедура отыскания характеристик описана в книге Уизема [Whitham, 1974]. Ниже мы приведем детали этой процедуры, опуская выкладки. Чтобы найти характеристики системы (6.3), запишем эти уравнения в векторном виде

1 п

(6.13)

(6.14)

Собственными значениями этой системы являются собственные значения матрицы [Л]. Последние определяются корнями характеристического уравнения матрицы

\[А]-Х[1]\ = 0 или 2

А]. Итак, мы записываем 1

=0.

-1 -Я

-Я -

Это приводит к квадратному уравнению Х-1/р2=0, корни которого суть Ki = 1/р, Х2 = - 1/р.

Эта пара корней образует дифференциальные уравнения характеристик (6.8), которые мы уже вывели. Так как исходное уравнение Прандтля - Глауэрта есть всего лишь волновое уравнение для ф, мы могли бы выписать дифференциальные уравнения характеристик, используя результаты нашего обсуждения дифференциального уравнения в частных производных второго порядка (2.15). Следующий шаг состоит в получении уравнений совместности. Следуя Уизему, эти уравнения можно получить, умножая систему (6.13) на левый собственный вектор матрицы [Л]. Это приводит к уравнениям, записанным вдоль характеристик.

Пусть L -левый собственный вектор матрицы [Л], отвечающий и и - левый собственный вектор, отвечающий Яг. Собственные векторы матрицы [А] находим из уравнения

Если положить

[lTh-V] = o.

(6.15)

[/}, ll]

1 П

= 0.

§ 6.2. Метод характеристик Это приводит к уравнениям

4 + /=о,

-L 1 L - о

Р2 -Г р - >

которые эквивалентны, как и ожидалось. Поскольку мы можем получить только нормализованные компоненты вектора l положим l\ = -р. Тогда

-Р 1

Аналогичным образом находим

Записывая систему (6.13) вдоль характеристик, получим теперь уравнения совместности. Для этого умножим уравнение (6.13) на транспонированный левый собственный вектор:

[lT[w, + H]w] = 0. (6.16)

В соответствии с уравнением (6.15) член [l][/l] можно заменить на [l]"Xj[/]. Поэтому мы можем переписать уравнение (6.16) в виде

[lT[w, + X,w,] = 0.

Уравнение совместности вдоль %\ получают из соотношения

[-Р, 1]

= 0.

Таким образом.

(P«-t) + (P«-.) = 0.

(6.17а)

Аналогичным образом уравнение совместности вдоль правой характеристики записывается в виде

(6.17Ь)

Уравнение (6.17а) справедливо вдоль положительной, или левой, характеристики. Оно выражает тот факт, что величина {u - v) остается постоянной вдоль характеристики, отвечающей