ДОЛЬНОЙ скорости Мх, которая равна 1, когда Mjc = 1, и больше 1, когда М; > 1 (рис. 8.4). Отсюда следует, что при Mjc > 1 продольный градиент давления может быть полностью включен в уравнение движения. Однако при Nix < 1 только часть этого члена, а именно (одр/дх, следует оставить с тем, чтобы собственные значения оставались вещественными и положительными. Заметим также, что о стремится к нулю вблизи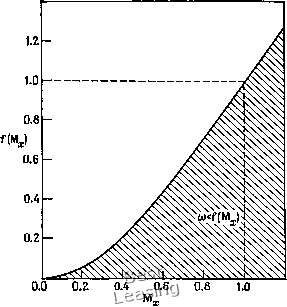

Рис. 8.4. Ограничение на изменение продольного градиента давления в дозвуковых областях потока.

стенки, где М; = 0. Таким образом, мы видим, что решения параболизованных уравнений Навье - Стокса, полученные маршевым методом по пространственной координате, подвержены неустойчивостям (расходящиеся решения), когда продольный градиент давления полностью сохраняется в дозвуковых частях пограничного слоя, так как тем самым вводится в них элемент эллиптичности. Предложены различные способы преодоления этой трудности, и мы их сейчас обсудим.

Самый очевидный способ борьбы с неустойчивостью - полностью отбросить градиент давления в дозвуковых зонах. Это даст устойчивую маршевую схему, но и приведет к ошибкам для полей течений с большими продольными градиентами давления. Следует, однако, заметить, что вариации давления в про-

ДОЛЬНОМ направлении будут по-прежнему сказываться на численном решении в случае, если давление определяется из уравнения движения по координате у и уравнения энергии. Альтернативный подход состоит в задании изменения продольного градиента давления. Очевидно, приравнивание нулю градиента давления - один из путей того, как это можно осуществить. Если продольный градиент давления определен, его можно исключить из матриц [А\\ и [А2]\ в уравнениях (8.44) и (8.48) и рассматривать как источниковый член в задаче нахождения собственных значений. Следовательно, продольный градиент давления уже не будет влиять на математическую природу уравнений. При решении уравнений пограничного слоя продольный градиент давления обычно известен из расчета внешнего течения невязкой жидкости или в случае внутренних течений определяется из закона сохранения массы. К сожалению, при решении параболизованных уравнений Навье - Стокса продольный градиент давления заранее неизвестен и должен вычисляться в процессе решения.

В некоторых работах продольный градиент давления был сохранен и в дозвуковых зонах и аппроксимировался разностями назад, которые рассчитываются с использованием информации с предыдущего слоя по маршевой координате. Например, когда рассчитывается решение на слое производная

др/дх представляется в виде

4 (8.53)

Т. е. это есть разность назад первого порядка. Лубард и Хел-лиуэлл [Lubard, Helliwell, 1973] исследовали устойчивость (расходимость), используя разности назад для продольного градиента давления в уравнениях движения и энергии. Они применили неявную разностную схему и показали при помощи анализа устойчивости по Фурье, что неустойчивость будет иметь место, если

x<(xUr. (8.54)

Это условие устойчивости очень необычно, так как обыкновенно из анализа устойчивости по Фурье вытекает, что неустойчивость будет иметь место, если Дл: больше некоторого (Ал:) max. Когда такой анализ был произведен для двумерных параболизованных уравнений Навье -Стокса (8.48) -(8.49), то оказалось, что

(AAt)mln =-vsin«(P/2)-•

где р -волновое число {kmy) Лубард и Хеллиуэлл показали также, что если продольный градиент давления аппроксимировать на неявном слое, как и все остальные члены параболизованных уравнений, то минимальный допустимый шаг (Ал:)т1п удваивается. Чтобы объяснить столь необычное условие устойчивости, Рубин [Rubin, 1981] высказал предположение, что (Ax)mfn является размером области передачи эллиптического взаимодействия вверх по потоку. Если (Дл:) > (Ал:)mm, то это взаимодействие как бы «не замечается» и маршевая процедура устойчива. В противном случае, если (Дл:) < (Дл:)пип, численное решение пытается учесть это эллиптическое взаимодействие, что ведет к расходящимся решениям, поскольку передача влияния вверх по потоку в маршевой процедуре запрещена. Рубин и Лин [Rubin, Lin, 1980] показали, что размер области эллиптического взаимодействия имеет порядок толщины дозвуковой зоны. Поэтому если дозвуковая зона сравнительно большая, то минимальная допустимая величина Дл: может быть слишком велика для осуществления точных (или устойчивых) вычислений.

Другой метод учета градиента давления в продольном направлении называется приближением подслоя. Первыми его предложили Рубин и Лин [Rubin, Lin, 1971], а позже он был применен для параболизованных уравнений Навье - Стокса Шиффом и Стегером [Schiff, Steger, 1979]. В приближении подслоя градиент давления в вязкой дозвуковой области вычисляется в точке вне подслоя, в которой скорость сверхзвуковая. Такое приближение основано на том, что в тонком дозвуковом вязком подслое др/ду пренебрежимо мало. Так как градиент давления задается в дозвуковой зоне, то маршевый по пространственной координате метод даст, видимо, устойчивое решение. Однако, как наблюдали Шифф и Стегер, в некоторых случаях возможны всё же расходящиеся решения. Они могут быть обусловлены взаимодействием через давление сверхзвуковых и дозвуковых областей, которое описывается нормальным уравнением движения и уравнением энергии.

Новый метод учета продольного градиента давления предложили Виньерон и др. [Vigneron et al., 1978а]. В этом подходе в дозвуковой вязкой зоне часть продольного градиента давления (i){dp/dx) в уравнении сохраняется, а остальная (1 - со) (др/дх) либо опускается, либо рассчитывается на явном слое при помощи разностей назад или приближения подслоя. Уравнение (8.41) переписывается в виде.

дЕ . дР , dF dFv /п