В направлении, параллельном стенке (уравнение движения по координате х), есть

дх др

которое дискретизируется следующим образом:

(9.136) (9.137)

(9.138)

Чтобы воспользоваться уравнением (9.138), необходимо знать давление хотя бы в одной точке на поверхности стенки. Давление в соседней точке можно определить при помощи аппроксимации первого порядка с односторонней разностью для др/дх в уравнении (9.137). После чего по уравнению (9.138) можно найти давление во всех остальных точках стенки. В случае системы координат, связанной с поверхностью стенки, запишем уравнение (9.137) в виде

(9.139)

где S измеряется вдоль поверхности тела, а л - по нормали к ней.

Описанный ранее метод установления для решения уравнения переноса завихренности и уравнения Пуассона требует, чтобы были заданы подходящие выражения для и на границах. Задание граничных условий для этих величин очень важно, так как они непосредственным образом влияют на устойчивость и точность решения. Рассмотрим постановку граничных условий на стенке, расположенной в плоскости у = 0. На поверхности стенки -ф есть константа, которую обычно полагают равной нулю. Чтобы найти g на стенке, разложим if в ряд Тейлора в окрестности точки (i, 1), расположенной на стенке:

*2 = М + 17

л i 1

Поскольку на непроницаемой границе

= Щ 1 = 0,

И по определению (9.122)

(9.140)

(9.141)

(9.142)

§ 9.3. Уравнения Навье -Стокса для несжимаемой жидкости 617 то уравнение (9.140) можно переписать как

,.= -Щ= + От. (9.143)

Это выражение первого порядка для i часто дает лучшие результаты, нежели выражения более высокого порядка, подверженные неустойчивостям при больших числах Рейнольдса. Например, следующее выражение второго порядка, впервые использованное Йенсеном [Jensen, 1959], приводит к неустойчивым вычислениям в диапазоне от умеренных до больших чисел Рейнольдса:

. = "-"/(У" + о тП (9.144)

Брили [Briley, 1970] объяснял неустойчивость, замечая, что выражение для в виде полинома, принятое при выводе уравнения (9.144), не согласуется с вычислениями и = д/ду в точке (/, 2 по центральной разности. Вычисляя и в точке (t, 2) по выражению

.II-+011. Р.И5)

которое согласуется с уравнением (9.144), Брили обнаружил, что его вычисления устойчивы даже при больших числах Рейнольдса.

Классической задачей с замкнутыми границами является расчет течения в полости с движущейся стенкой, показанной на рис. 9.3. В этой задаче вязкая несжимаемая жидкость в полости приводится в движение движущейся верхней стенкой. Граничные условия для этой задачи указаны на рис. 9.3. Задача о течении в полости с движущейся стенкой является прекрасным тестом для сравнения разных, методов решения уравнений Навье - Стокса для несжимаемой жидкости. Обычным тестовым условием является условие Re/ = 100, где

Re = f /v (9.146)

и / - ширина полости. Подробные результаты вычислений можно найти в работах [Burggraf, 1966; Bozeman, Dalton, 1973; Rubin, Harris, 1975], результаты эксперимента - в работах [Mills, 1965; Pan, Acrivos, 1967].

Очень важно правильное задание значений g и на границах различного типа, таких, как линии симметрии, свободные

поверхности, входная и выходная плоскости, линии, на которых задается условие непротекания, и т. д.; кроме того, следует быть особенно внимательным, чтобы правильно моделировать физику течения. В монографии Роуча [Roache, 1972] имеется превосходный обзор постановки граничных условий самого разного типа.

Альтернативный способ решения уравнений Навье -Стокса для несжимаемой жидкости, записанных в переменных завих-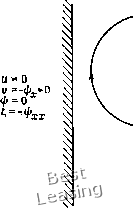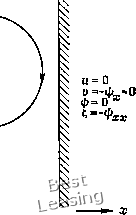

Рис. 9.3. Задача о течении в полости с движущейся стенкой.

ренность - функция тока, связан с использованием стационарного уравнения переноса завихренности

(9.147)

Это эллиптическое уравнение можно решать методами, аналогичными применяемым для уравнения Пуассона. Такой подход с успехом использовался некоторыми специалистами, но оказалось, что он приводит к неустойчивостям. Поэтому вместо решения стационарных уравнений рекомендуется пользоваться методом установления.

Распространение подхода с использованием завихренности и функции тока в качестве независимых переменных на трехмер-