х = - -

(10.5) (10.6)

В только что рассмотренном примере преобразование было аналитическим и с его помощью сразу получили распределение

= 0.Z5 Л7 = 0.25

Рис. 10.3. Расчетная сетка в физической плоскости.

узлов сетки. Можно было бы построить такое же преобразование, задавая точки в физической плоскости вдоль линий постоянства I и т] и численно вычисляя метрические коэффициенты с использованием центральных разностей. Это имеет то преимущество, что можно задавать точки в любом месте физической плоскости. В этом случае преобразование будет численным, а не алгебраическим.

Если преобразование задается численным образом, то х, лг, У1 и рассчитываются разностными методами. В дифференциальном уравнении, которое следует решить, фигурируют величины 1ху 1уу у]х и цу. Их определяют из выражений

1и = -

(10.7)

Подробнее об этом будет говориться ниже, где рассматриваются методы построения расчетных сеток путем решения дифференциальных уравнений.

рассчитываемые по уравнениям (10.4), имеют вид

затем

и, наконец.

1-Ш75 2.6250

• = -Ж--0-85714.

В этом примере численный и аналитический расчеты дают одинаково хорошие результаты. Конечно же, это не всегда так.

Пример 10.3. Изображенная на рис. 10.4 область в форме трапеции отображается на прямоугольную область, заданную следующими уравнениями:

\+1 з-ч

у 2 •

Здесь физическая область отображается на прямоугольник с центром в начале координат. Это пример нормализующего преобразования по одному направлению и последующего параллельного переноса. Понятно, что любая четырехугольная форма может быть отражена на прямоугольник в вычислительной области использованием нормализующего преобразования.

Для построения требуемых расчетых сеток можно использовать очень сложные алгебраические функции. Смит и Вейгель [Smith, Weigel, 1980] разработали гибкий метод построения сеток. В нем две несвязанные границы отображаются из плоскости прямоугольных физических координат на вычислительную плоскость. Пусть в физической плоскости две несвязанные гра-

Пример 10.2. Вычислить метрические коэффициенты только что рассмотренного простого нормализующего преобразования аналитически и численно.

Метрические коэффициенты будем вычислять в точке (1.75, 2.2969) (см. рис. 10.3). Аналитический расчет по уравнению (10.5) дает

2 (0.75) . --Г75~" -0.85714.

Численный расчет будем проводить по уравнению (10.7). Сначала вычислим якобиан

, 3.0625- 1.53125 о лспсл / = хУ - УгХг, =-щщ-= 3.06250,

(10.9)

ницы задаются уравнениями

Xbi = Xi(1), Ув\=уЛ1),

ХВ2 = Х2{1), г/в2=«/2(1).

в вычислительной плоскости изменяется на отрезке О 1 и преобразование определяется так, что при т] = О

Хвх = хЛ1) = х(1, 0),

Увх=Ух{1) = У(1, 0)

и при Т1 = 1

XB. = X2==xil, 1),

Ув = УЛ1) = У{1, О-Некоторая функция, определенная при О т)

1 и зависящая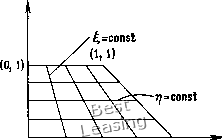

(0,0) (2,0)

Рис. 10.4. Область в форме трапеции в физической плоскости.

от параметров на двух границах, задается алгебраическими выражениями в виде

y = yil ri)=G(y„ .....у„ ...).

(10.11)

Смит и Вейгель предлагают использовать полиномы второй или третьей степени. Если выбрать линейную функцию, то

у=ухти-г\)+уЛ)г\. -

Пример 10.4. Чтобы на практике показать применение этого подхода, отобразим трапецию, задаваемую уравнениями

л: = 0, л:=1, у = 0, у=1+х,