С Граничными условиями

г = го, л = 1; е = о, 1 = 1;

r = ri, Л = Птах; 9 = 2Я, 1 = 1тах

Решение имеет вид

х==Нсовфу у = R sin фу

Imax

Интересно, что в этом случае решение не дает равномерной сетки в физической области. Сетка оказывается набором концен-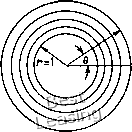

2.0 1-5 1.0 I-

1.5 (Ь)

Рис. 10.5. Применение метода Томпсона: (а) физическая плоскость; (Ь) вычислительная плоскость.

трических окружностей. Чтобы сделать эти окружности равноотстоящими друг от друга, следует задать Р = 0 и Q = 1/ц (см. задачу 10.9).

Как отмечалось ранее, одна из трудностей применения этого метода заключается в контроле размещения узлов внутри области. Для получения желаемого распределения узлов необходимо располагать методикой задания Р и Q. Миддлкофф и Томас [Middlecoff, Thomas, 1979] разработали методику, которая обеспечивает приближенный контроль размещения узлов сетки путем оценки Р и Q по требуемому распределению точек на границе.

Чтобы пояснить эту идею, предположим, что требуется решить уравнение (10.15) с условиями Дирихле. Выберем следующую форму записи Р и Q:

Р = Ф(1. +

§ 10.3. Методы, основанные на решении дифференциальных уравнений 641

где ф и будут определены ниже из граничных условий. С учетом этого исходную систему уравнения (10.15) можно записать в виде

«(Уц + ФУг) - 2Рул + Y Кг, + Уг) = 0. Приравнивая выражения, стоящие в скобках, нулю на границе, определяем функции и г). Миддлкофф и Томас требуют, например, чтобы вдоль границы g = const выполнялись условия

(10.19)

а вдоль границы 11 = const - условия

""in (10.20)

Поскольку X и у известны во всех точках границы, то функции и 1) могут быть определены с использованием центрально-разностной аппроксимации для всех производных, входящих в уравнения (10.19) и (10.20). Следует отметить, что и -ф определяют по одному из уравнений каждой пары (10.19) и (10.20). Обычно если ф находят по одному из уравнений (10.20), то другое при этом отлично от нуля. То же справедливо и в отношении функции г), которую определяют из уравнений (10.19). Используя такой подход, находят функции и г) на границе, а внутри области значения этих функций получают простой экстраполяцией. Данная методика дает способ управления распределением внутренних узлов по требуемому их распределению на границе. Предложены и другие методы контроля распределения узлов сетки. Можно рекомендовать работы [Thompson et al., 1975; Thompson, 1980], где дан обзор наиболее удачных из них.

Для построения расчетных сеток могут быть использованы уравнения с частными производными других типов. Стегер и Соренсон [Steger, Sorenson, 1980] описали метод, использующий систему гиперболических уравнений для построения сетки вокруг некоторого тела. При этом внешняя граница заранее не указывается. Поверхность тела образует внутреннюю границу, и система гиперболических уравнений решается маршевым методом в направлении от тела, что не требует задания внешней границы. Стегер и Соренсон предлагают метод дуг и метод объемов, приводящие к построению ортогональных сеток. Остановимся подробнее на последнем.

В случае двух измерений якобиан преобразования дает отношение площадей ячеек сеток в физической и вычислительной плоскостях. Если считать, что размеры ячейки сетки в вычисли-

тельной плоскости равны единице (Д = Дт) = 1), то ее площадь также равна единице. Тогда величина

НУг-У1Хг = (10.21)

есть площадь ячейки сетки в физической области. Если / считать функцией координат, то уравнение (10.21) можно использовать как одно из уравнений для контроля сетки в физической области. Второе уравнение получаем из условия ортогональности линий сетки к границе в физическом пространстве. Поэтому вдоль границы (л:, t/) = const можем записать

Вдоль линии т] = const

dy dx

S-const

(10.22)

(10,23)

Ti=const Ч

Если ЛИНИИ постоянства g и т) перпендикулярны, то на плоскости JC, у должно выполняться соотношение между тангенсами углов наклона этих линий

"X /c=const ч-const

ИЛИ С учетом (10.22), (10.23)

XiXr, +У1Уу = . (10.24)

Система уравнений (10.21) и (10.24) линеаризуется разложением в ряд вокруг некоторого известного состояния [х, у). Один из членов уравнения (10.21) запишется так:

Х1У = {х + х - х\{у + у - у\ =

= + Ч) + h К (А2) =

= Угх + ЧУг - НН + о (А). (10.25)

Если остальные члены линеаризовать аналогичным образом, то получим

H]W + [B]w = f. (10.26)

[А] =

1-4 -УпУ

[В] =

L/ + 7J

(10.27)