числительной ~ через , т, то уравнение для скорости движения узлов можно записать в таком виде:

W,--

где e - некоторая мера локальной ошибки, а нижний индекс av означает усреднение по всем узлам сетки, г?/- расстояние между узлами i и j, возведенное в степень п. Константа k в этом уравнении произвольна, так как не существует физического закона, связывающего скорость движения узлов и ошибку. Одна из основных трудностей применения этого метода состоит в определении подходящим образом меры ошибки. Рай и Андерсон предлагают взять за нее ошибку аппроксимации в дифференциальном приближении разностной схемы. Чтобы иметь лучшее разрешение, они использовали также градиенты вместо локальной ошибки. Благодаря достаточно общему представлению скорости движения узлов в уравнении (10.52), любой разумный выбор е можно использовать для управления движением сетки. Следует считать, что уравнение (10.52) задает метод равномерного распределения ошибки по сетке. При этом вычисляемую скорость узлов можно интерпретировать как остаточный член численного решения на сетке, удовлетворяющей некоторому закону эквираспределения.

Хотя одномерные примеры не отражают всей сложности задач построения сеток более высокой размерности, они все же демонстрируют эффект применения адаптивных сеток. Нестационарное вязкое уравнение Бюргерса

Щ + wwjc = Vxx (10.53)

с начальными условиями

г 1,

и{0,х) = [ О

И граничными условиями

u(t, 0)=1, u{ty 1) = 0

решали, используя в уравнении (10.52) градиенты в качестве в, т. е. меры локальной ошибки. Результаты численного решения уравнения Бюргерса можно сравнить с точным аналитическим решением

u = uth

где й находят из решения

(й-1)/(й+1) = в- Re = 1/р.

Последнее описывает стационарный случай, причем его наклон на правом конце интервала тем круче, чем больше число Рейнольдса. На рис. 10.8 и 10.9 показаны результаты расчета при двух разных значениях числа Рейнольдса. Очевидно, что применение адаптивных сеток приводит к уменьшению ошибки в обоих примерах. Следует отметить, что решение сглаживается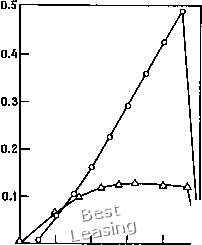

0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0

Рис. 10.8. Величина ошибки в процентах в расчете при Re = 2; х-- физическая координата; О неадаптивная сетка, Л адаптивная сетка.

Рис. 10.9. Величина ошибки в процентах в расчете при Re = 3; обозначения см. в подписях к рис. 10.8.

прежде, чем успевают выработаться градиенты. Это обеспечивает лучший контроль за движением узлов сетки. Если сглаживание не производить, то полученные результаты расчета будут сильно осциллировать.

Метод построения расчетной сетки путем задания скорости движения узлов легко распространить на случай двух измерений. Если для It воспользоваться уравнением типа уравнения (10.52), то можно вывести аналогичное выражение для r\t, в котором величины зависят только от производных по направлениям I или Т1, причем r\t зависит только от производных зависи-

б.00

мых переменных по направлению ц. Для преобразования вида

= т, 1 = 1{х, у, t), Т1 = т)(л:, у, t)

получаем

Хх- J .Ух- J > (10 54)

J = lxy-xlx

Уравнения (10.54) позволяют вычислять скорость движения узлов сетки в физическом пространстве. На рис. 10.10 изображена

сетка, использованная в задаче расчета сверхзвукового обтекания цилиндра невязкой жидкостью. Эта задача была решена с использованием как неподвижной, так и адаптивной сеток. При построении адаптивной сетки использовалась информация о величине градиента численного решения (рис. 10.11).

Так как точное решение задачи неизвестно, то за основу при сравнении было взято численное решение, полученное на неподвижной сетке размером 19X19. Можно видеть, что ошибки численного решения уменьшаются даже в том случае, когда адаптивная сетка не слишком отличается от неподвижной. Очевидно, что схемы с применением адаптивных сеток пригодны и для трехмерных задач. Однако для построения полностью трехмерной сетки требуется совсем другое уравнение для скорости движения узлов.

Иногда бывает трудно подобрать подходящую меру величины ошибки для контроля построения сетки. Как отмечалось ранее, такой мерой, видимо, является первый член ошибки аппроксимации дифференциального приближения разностной схемы. Клопфер и Макрэй [Klopfer, McRae, 1981b] получили ошибку аппроксимации дифференциальных приближений разностных схем для решения уравнений Эйлера. Они использовали ее в качестве меры ошибки численного решения при построении сетки в примерах с одним измерением. В некоторых

0.00

-3.00 0.00

Рис. 10.10. Адаптивная сетка для задачи расчета обтекания цилиндра в физических координатах х, у.