На рис. 10.14 приведено распределение давления вдоль центральной линии канала, рассчитанное на неподвижной и адаптивной сетках. Осцилляции, имеющие место в расчетах на не-подвияной сетке, типичны для методов сквозного счета второго порядка. Однако они отсутствуют в установившемся решении при использовании сетки, адаптированной к положению скачка.

Можно привести еще один пример: однородный сверхзвуковой свободный поток с косым скачком, который также демонстрирует свойство этой схемы выстраивать сетку динамически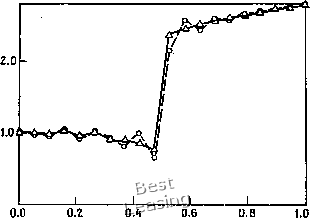

Рис. 10.14. Распределение давления вдоль оси симметрии канала; А -

решение, полученное на адаптивной сетке размером 20 X 7;--О--Решение, полученное на неподвижной сетке размером 20X7; /exit = 0.1.

В процессе решения, сообразуясь с положением скачка. Это течение изображено на рис. 10.15. Так как задача является полностью сверхзвуковой, то мы не испытываем трудностей с заданием граничных условий на выходе и решаем уравнения Эйлера, зависящие от времени, записанные в дивергентной форме, на сетке, показанной на рисунке. Локально адаптированная к скачку сетка изображена на рис. 10.16. На рис. 10.17 показаны профили давления при t/ = 0, рассчитанные на неподвижной и адаптивной сетках. Отметим еще раз удивительный факт отсутствия осцилляции у численного решения, полученного на сетке, адаптированной к положению скачка. Подход с использованием сеток последнего типа имеет очевидные преимущества при использовании схем сквозного счета.

В настоящем разделе мы ввели понятие о сетках, адаптированных к решению. Численное решение уравнений с частными

Производными на адаптивных сетках приводит к существенному улучшению точности. Помимо изложенных методов находят

0.0 0.1 О.г 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Рис. 10.15. Неподвижная сетка для задачи расчета однородного сверхзвукового течения с косым скачком.

0.0 П.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Рис. 10.16. Сетка, адаптированная к положению скачка, для задачи расчета однородного сверхзвукового течения с косым скачком.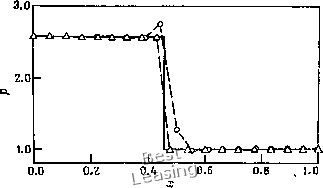

Рис. 10.17. Распределение давления в плоскости у = 0 для однородного сверхзвукового течения с косым скачком, - аналитическое решение; - А -

решение, полученное на адаптивной сетке размером 19X7;--О--решение, полученное на неподвижной сетке размером 19X7.

применение и другие подходы. Идеи, используемые при конструировании схем с адаптивными сетками, ограничены лишь возможностями человеческого воображения, и любая схема, приводящая к более точным результатам, является приемлемой.

§ 10.5. Дополнительные соображения

Закончим главу о построении расчетных сеток замечанием, что сетка, построенная для решения некоторой конкретной задачи, должна быть соответствующим образом связана с дифференциальными уравнениями в частных производных. Эта связь осуществляется через метрические коэффициенты преобразования, возникающие в этих уравнениях.

Рассмотрим уравнения Навье -Стокса для сжимаемой жидкости, записанные в строго дивергентной форме (см. уравнение (5.240)). Пусть исходная система координат прямоугольная. Перейдем от нее к криволинейной системе координат (т, g, т), ) и для простоты ограничимся рассмотрением уравнений течения невязкой жидкости. В случае двух измерений уравнения (5.240) можно записать в виде

W (т) + ж t" - "" + .Е - яР] +

+ -щ- [{х.Уг - УгХг) и - г/Е + xF] = 0. (ю.бо)

Заменим теперь дифференциальные операторы конечно-разностными операторами Г и запишем дискретный аналог уравнения (5.240) для однородного течения (т. е. заменим зависимые переменные постоянными величинами). Это приводит к следующим соотношениям:

Г, (-)-) + {Угг, - + iy - = 0> (10-61)

lKO-r,(xf) = 0. (10.63)

Нижний индекс разностного оператора обозначает дискретизацию по времени или пространству, а верхние индексы (1) и (2) указывают на два различных численных представления одной и той же величины.

Уравнения (10.62) и (10.63) тождественно удовлетворяются, если они дискретизируются по той же схеме, что и уравнение (10.61). Уравнение (10.61) представляет собой дискретизацию тождества, названного Томасом и Ломбардом [Thomas, Lombard, 1978] геометрическим законом сохранения. Дифференциальный аналог этого выражения имеет вид

4г{т)+-к (" +"""~ "=

и его следует дискретизировать точно так же, как и уравнения однородного течения (уравнение (10.61)). Очевидно, это уравне-