значению переменной. Это применимо к случайному блужданию, поскольку все изменения при нулевом сдвиге имеют математическое ожидание, равное нулю.

По сути мартингал - это более общий стохастический процесс, чем случайное блуждание, потому что в случае мартингала изменения задаются значением случайной переменной, которая хотя и должна обладать нулевым математическим ожиданием, но не обязательно должна иметь постоянную дисперсию. Кроме того, изменения не должны быть независимыми.

Случайное блуждание с положительным сдвигом является примером субмартингала. При отрицательном сдвиге это будет примером супрамартингала.

Например, рассмотрим процесс, определенный как

Г,= Г, , + 0,8 + е. Это пример субмартингала. В общем виде это выглядит как У, - У,-\ + а + е; (7.3)

если а>0, то мы имеем дело с субмартингалом,

если а<0, то это супрамартингал;

если же а = 0, то это будет случайное блуждание. Графики примеров случайного блуждания, субмартингалов и

супрамартингалов приведены на рис. 7.1-7.3.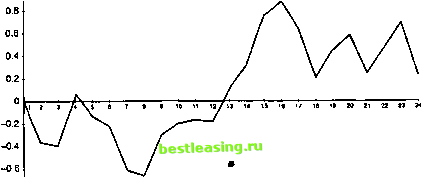

-0.3

Рис. 7.1. Случайное блуждание

Анализ временных рядов 3 -) 7

1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 19 20 21 22 23 24

Рис. 7.2. Субмартингал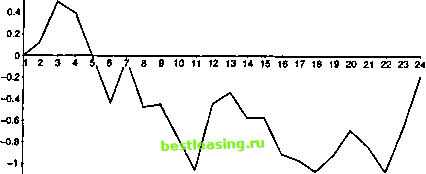

-1.21-

Рис. 7. 3. Супрамартингал

Белый шум

Временные ряды называются белым шумом , если лежащая в их основе переменная имеет среднюю, равную нулю, постоянную дисперсию и нулевую корреляцию последовательных наблюдений, т.е. нулевую автокорреляцию. Вы помните из гл. 6, что допущения для значения остаточного члена регрессионной модели МНК схожи с этим. Таким образом, остатки рассматриваемые в МНК, можно считать белым шумом .

Если E(zt) ~ N(0, ст2), то мы имеем дело с гауссовским белым шумом, хотя переменная белого шума необязательно должна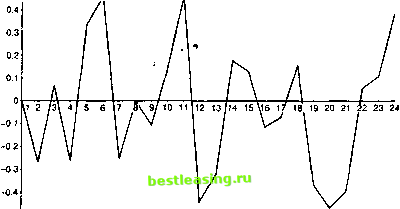

-0.5

Ряс. 7.4. Белый шум

Стационарность

Временные ряды называются стационарными, если они обладают постоянной средней и дисперсией, а ковариация зависит только от временного интервала между двумя отдельными наблюдениями.

Возьмем, например, индекс FTSE 100. Этот индекс возрос с уровня 1000 на момент открытия до 3600 на момент написания этой книги, спустя 12 лет. Представьте, что вы анализируете среднюю и среднее квадратическое отклонение дневного уровня за каждый календарный год. Поскольку индекс возрастает год за годом, то средняя величина и среднее квадратическое отклонение в течение первого года будут ниже, чем в течение второго года и т.д., и очевидно, что в тот год, когда индекс возрос до 3500, затем упал до 3100, средний уровень будет выше, чем в первый год начала исчисления индекса.

В гл. 2 мы отметили, что величина дисперсии и среднего квадратического отклонения может быть функцией от значения индекса. Таким образом, дисперсия индекса, колеблющаяся вокруг 1000, вполне может быть ниже дисперсии индекса, колеблющегося вокруг отметки 3000.

Пример белого шума изображен на рис. 7.4.