xe+1=x-fixn)/f\x ). (8.10)

То есть результат каждой итерации находится через вычитание из результата по предыдущей итерации отношения функции Дх) к ее первой производной f(x). Однако это не срабатывает только тогда, когда случайным образом одна из хп является точкой, в которой f(x ) равно или близко к нулю (в этом случае, начав процедуру заново с того момента, когда произошел сбой, из новой точки, вы почти всегда решите возникшую проблему).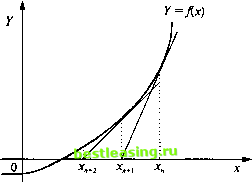

Рис. 8.2

Можно утверждать, что недостаток метода - необходимость предварительного нахождения f(x). Однако этого можно избежать, если заменить f(x) на конечное разностное приближение:

/(х + И) - Дх) И

(8.П)

где h очень мало и может уменьшаться при выполнении итерационного процесса. Следовательно, теперь в процесс может быть введен компьютер, чтобы рассчитать J[xn) и J[xn + h) (для текущих значений хп и я) и оценить

/(* )

f(xn+h)-f(xn) И

(8.12)

Принимая во внимание сложность и продвинутость современных компьютерных алгебраических пакетов программ (которые должны были бы называться алгебраическо-вычи-слительными пакетами программ!), непосредственный расчет может производиться автоматически.

Теперь применим процедуру Ньютона-Рафсона к оценке облигации со сроком погашения 2,5 года. Мы уже отметили, что функция f(x) - 0 для этой облигации будет являться многочленом пятой степени, а именно:

Ах) = 98х5-5х4-5х3-5х2-5х-105 = 0. (8.13)

В начале итеративного процесса мы предполагаем, что х = 1,055. Заменив х на 1,055 в выражении (8.13), получим следующий результат:

fix) =98 1,0555-5 1,0554-5 1,0553-5

1,0552-5 1,055-105 =0,176625.

Мы должны скорректировать 1,055 в соответствии с результатом 0,176625 и значением первой производной функции (8.13) 551,2939. Тогда х\ - значение х во второй итерации равно

Повторное вычисление по формуле (8.12), но на этот раз для значения 1,054680 в качестве х, дает следующее:

fix) = 98 1,054680s-5 1, 0546804-5 1, 0546803-

-5 1, 0546802-5 1, 054680-105 =0,0001125. (8.14)

Далее мы корректируем 1,054680 в соответствии с результатом 0,0001125 и значением первой производной функции (8.14), равным 550,5916, и получаем х2 - значение х в третьей итерации:

Повторное вычисление по формуле (8.12) при х - 1,054679 дает

f(x) =98 1,054679s-5 1, 0546794-5 1, 0546793--5 1, 0546792-5 1, 054679-105 =0,000017.

Следовательно, х - 1,054679 для j\x) - 0 с требуемой точно стью до четырех десятичных знаков.

Однако вспомним, что нам нужно найти годовое значени* IRR для облигации со сроком погашения 2,5 года, пока же мь только нашли IRR для полугодовых периодов. Поэтому значение х необходимо возвести.вквадрат (х2) для получения искомого 1 + IRR. Значит, 1 + IRR = 1.0546792 = 1,112348. Это означает, что полный доход при погашении для данной облигации равен 11,2348%. Мы получили точно такой же результат, что и при использовании метода деления пополам, однако он был получен с помощью гораздо меньшего числа итераций.

Из гл. 3 мы помним, что в процессе интегрирования находится площадь под кривой, а первый этап этого процесса - нахождение первообразной интегрируемой функции. Затем определяется значение первообразной функции в конечных точках интервала для нахождения площади. К сожалению, для множества функций не существует первообразных, хотя это не означает, что не существует и интеграла.

Вспомним из гл. 4, что функция

это вероятность нормально распределенной переменной принять значение от 1 до 2. Значение этого интеграла представлено в виде заштрихованной области на рис. 8.3.

Поскольку не существует такой функции J{x), чтобы

методы интегрального исчисления, приведенные в гл. 3, не могут быть использованы, следовательно, необходимо применить численные методы. Покажем два из них. Они заключаются в разбиении площади под кривой на маленькие вертикальные полоски, высота которых равна расстоянию между данной точкой на гори-

ЧИСЛЕННЫЕ МЕТОПЫ ИНТЕГРИРОВАНИЯ

(8.15)

(8.16)