зонтальной оси и кривой. Затем рассчитывается площадь каждой из полосок, а их сумма приближенно равна площади под кривой.

Рис. 8.3

Правило трапеции

Первый метод, который мы продемонстрируем, использует правило трапеций. Согласно этому подходу искомая площадь под кривой разбивается на множество вертикальных узких полосок равной ширины (рис. 8.4). Если каждая линия соединяется сверху с другой линией, полученная форма будет трапецией, которая приближенно соответствует фактической площади под кривой между вертикальными линиями.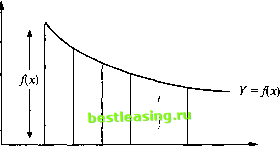

О 1,0 1,2 1,4 1,6 1,8 2,0 х

А-►

Рис. 8.4

Так как на данном интервале кривая вогнута, то площадь каждой трапеции немного больше фактической площади под кривой между соответствующими линиями. Таким образом, сумма площадей трапеций будет переоценивать искомую площадь. Если бы кривая была выпуклой, площадь трапеций недооценивала бы фактическою площадь под кривой. Этот вид ошибки может быть уменьшен посредством использования большего количества интервалов. Продемонстрируем это позже.

Каждая вертикальная линия выходит из точки х на оси абсцисс, соответствующей аргументу функции Дх). Высота линии определяется значением функции Дх). Тогда площадь трапеции рассчитывается исходя из оценки каждой пары fix), например, при Дх = 1,0) и Дх = 1,2) (рис. 8.4) путем нахождения средней этих двух величин (высот) и умножением ее на ширину трапеции (0,2 в нашем примере). В результате площадь под кривой приближенно определяется суммой площадей трапеций.

Для иллюстрации подхода найдем площадь под кривой между точками 1 и 2. Разобьем пространство между ними на пять интервалов.

Если площадь трапеции определяется произведением средней высоты на ширину, тогда общая площадь будет:

/(1,0) + /(1,2)

/(1,2)+ /(1,4)

0,2

/(1,4)+ /(1,6)

0,2

/(1,6)+ /(1,8)

0,2

/(1,8)+ /(2,0)

Эту функцию можно представить и в более компактной форме: -1Д1,0) + Д2,0) + 2(Д1,2) + Д1,4) + Д1,6) + Д1,8))].

Общий же вид формулы следующий:

Л/2( конечные значения + 2 внутренние значения ), (8.17)

где h - ширина каждой из трапеций, конечные значения обозначают сумму значений функции в граничных точках, а за внутренние значения принимается сумма значений функции в остальных (внутренних) точках интервала.

мы, прежде всего, находим значение функции f(x) для каждого из значений х, разделяющих интервал на пять частей:

х 1 1,2 1,4 1,6 1,8 2

/(*) = =<Г*2/2 0,2420 0,1942 0,1497 0,1109 0,0790 0,0540

h =0,2,

граничные значения = 0,2420 + 0,0540 = 0,2960, внутренние значения =0,1942 + 0,1497 + 0,1109 + 0,0790 =0,5338.

Тогда

j-jLe-x2/2*(0,2960 + 2 0,5338) =0,1364.

Ранее мы отметили, что точность этого метода может быть улучшена за счет увеличения числа полосок. Поэтому, используя этот же пример, проделаем вычисления снова, но на этот раз для десяти интервалов.

внутренние значения = 0,2179 + 0,1942 + 0,1714 + 0,1497 +

+ 0,1295 + 0,1109 + 0,0940 +

+ 0,0790 + 0,0656 = 1,2122.

Тогда

\~е-х2<2*Ц- (0,2960 + 2 1,2122) =0,1360. >/2я 2

Следовательно, для нахождения интеграла

г 1 .е-*11