3. найти сумму полученных выше результатов для получения стоимости опциона.

Используя ту же информацию, что и в четырехпериодном биномиальном процессе, стоимость опциона на покупку можно определить суммой следующих пял выражений.

Результат после четырех движений вверх (и4):

---0,595394(0,40461)4-4[17,21]

4Л4~4)---= 1,967 .

(1.024)4

Результат после трех движений вверх и одного движения вниз (иъй):

--41-- 0,595393 (0,40461)4 3 [ 7,75]

3!<4-3)!--4-= 2,408 .

(1,024)4

Результат после двух движений вверх и двух движений вниз (u2d2):

4! <1л2,Л/,Л/<с,ч4-2

-0,595392 (0,40461Г 2[0]

2 .(4-2)1 = 0

(1,024)4

Результат после одного движения вверх и трех движений вниз (и 3):

- 0,59539 (0,40461Г-[0]

1!(4-1)!

(1,024)4

Результат после четырех движений вниз ( 4):

4! Л .. -О/л /in/nci\4-0r

г0,59539и(0,404б1),-и[0]

0!(4-0)! = 0

(1.024)4

Суммирование этих значений дает точно такой же результат, что и по методу, применявшемуся ранее, т.е. получаем величину 4,37 с точностью до сотых.

В этих примерах предполагалось, что срок действия опциона разбивается лишь на четыре дискретных временных периода. В действительности же время до момента исполнения может быть разделено на множество бесконечно малых временных периодов. Чем больше количество периодов, тем больше степень точности

расчетов. Для того чтобы это продемонстрировать, разделим одногодичный срок на 6, 10, 20, 40 и 100 периодов, тогда цены опциона на покупку будут 4,5256, 4,5723, 4,6081, 4,6262 и 4,6371 соответственно. Сравним эти результаты со значением 4,6446, полученным по модели Блэка-Сколса, предусматривающей непрерывный во времени процесс. Таким образом, ошибка для 100-периодной биномиальной модели составила всего 0,0075 единиц опционной премии.

Таким образом, можно отметить интересное обстоятельство, что с уменьшением временного интервала каждого биномиального испытания (т.е. с возрастанием п) процесс приближается к , непрерывному во времени стохастическому процессу получения дохода по активу, который описывается моделью Блэка-Сколса. Эта модель будет описана в гл. 10, охватывающей финансовую математику непрерывных процессов.

Триномиальный эквивалент биномиальной модели ценообразования опционов

Биномиальная модель ценообразования опционов имеет преимущество умеренной интуитивности и большой гибкости по отношению к опционам, к которым она может быть применена. Однако у нее есть и недостаток - медленное получение результата по сравнению с другими моделями, имеющими однозначное решение.

Представим триномиальный эквивалент биномиальной модели. Эта модель обладает такой же гибкостью, что и оиномиаль-ная, но опционная премия рассчитывается быстрее.

В триномиальном процессе цена на основной актив может принять три возможных значения в конце каждого триномиального испытания. Она может возрасти согласно коэффициенту и и составить Su, остаться на том же уровне Sq или упасть до Sd, где d = 1/и.

Для того чтобы учесть допущение, что опционы оцениваются в безрисковой среде, а актив следует логнормальному распределению, мы должны скорректировать значения и и d (q равно единице по определению):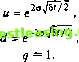

(8.36)

Однопериодная триномиальная модель ценообразования имеет вид:

р.. си + pacq + pdcd

С = --*у и . (8.37)

Так же как и родственная биномиальная модель, эта модель может применяться для опционов на покупку и на продажу исходя из ограничивающих условий:

C = max [S-X,0],

Р = тах [Х- S,0].

Перед тем как применить эту модель, мы должны рассчитать величины ри, pq и рф Первый шаг - расчет р, определяемого как

С е (8.38)

e V5/2 e-w8/2

Затем рассчитываем ри - р1, рд = 2р(\-р) и pj = (1-р)2.

Для того чтобы проиллюстрировать преимущество экономии времени этой модели, построим двухпериодное дерево и покажем, что точность результата будет такой же, что и при построении четырехпериодного биномиального дерева.

Рис. 8.11 изображает двухпериодное дерево для цены основного актива и стоимости соответствующего опциона на покупку, где S = 35, X = 35, г = 0,09525, волатильность = 0,2 и (T-t) = 1,0.

Используя выражение (8.37), а также значения параметров, приведенных на рисунке, вместе с конечными значениями для цен активов, стоимости опциона в трех узлах (си, cq и cd) во время г + 1, найдем так же, как и при биномиальном подходе. Например, стоимость опциона на покупку си:

0,354396 17,2114 + 0,481831 7,7491 + 0,163773 0 си =---- 9,3769,

а стоимость опциона на покупку cq:

0,354396 7,7491 + 0,481831 -0 + 0,163773 0 -co1, cq =- -= 2,6816 .

Ясно, что значение cd равно нулю.