OWl (все активы должны иметь неотрицательные веса) (9.10) OWl

3. Wa + Wb+ Wc= \ (средства должны быть полностью

инвестированы) (9.11)

Заметьте, что все ограничения линейны (т.е. нет величин во второй или более высоких степенях) и одновременно присутствуют ограничения в виде равенств и неравенств.

Мы продемонстрируем приложение линейного программирования, показав, как вышеозначенная задача решается сначала графически, а затем симплексным методом.

Графическое решение

Для иллюстрации графического решения мы используем третье ограничение, чтобы исключить Wc и тем самым получить задачу с двумя переменными. Это возможно, потому что в каждой портфельной задаче, где средства полностью инвестируются в портфель, если мы знаем я-1 весов, то можно определить л-ный вес. Так как все веса должны в сумме дать единицу, то л-ный вес равен

Заметьте, что этот переход от трех к двум переменным происходит только по причине облегчения графической демонстрации метода. Задача в том виде, в котором она была сформулирована, будет скорее всего передана ЛП - пакету в ее первоначальной форме - преобразования, сокращающее число переменных, обычно не проводятся.

Используя ограничение Wa + Wb + Wc = 1 для замены Wc на \-Wa-Wb, переопределим целевую функцию: максимизировать

0,11 Wa + 0,15 Wb + 0,08( 1 - Wa- Щ = 0,03 Wa + 0,07 Wb + 0,08 (9.12)

1 Wa + \,lWb + 0,9(1-И/-И/6) * i,i

0 <, Wa 1 (9.13)

0<L\Vb<L\

Если считать вес актива С как остаток, мы можем максимизировать следующую целевую функцию:

Когда мы найдем оптимальные веса для А и В из этой функции, мы сможем вычесть сумму этих весов из целого и найти вес актива С.

Заметьте, что +0,08 является константой. Как таковую нам не нужно включать ее в функцию для максимизации, потому что, если мы найдем значения Wa и Wb, которые максимизируют 0,03 Wa + 0,07 Wb, то найдем и значения, максимизирующие 0,03 Wa + 0,07 Wi, + 0,08. Поэтому, как только мы максимизируем 0,03 Wa + 0,07 Wb, то сразу же следует прибавить константу 0,08.

Так как мы заменили выражение для С в целевой функции, необходимо сделать то же самое и с ограничениями. Следовательно, ограничения становятся следующими

Заметьте, что как и в целевой функции, мы удалили величину В актива С из В активов А и В. Мы также устранили влияние В актива С на максимальное В портфеля.

При нахождении графического решения (рис. 9.1) мы стремимся определить область возможных решений между двумя осями, которыми в данном примере являются Wa и W

По второму ограничению максимальная пропорция, которую мы можем инвестировать в А, составляет 100% или единицу. Это показано точкой N. Аналогично точка А отражает 100% портфеля, инвестированные в актив В. Так как и Wa, и Wb должны быть меньше или равны единице, вертикальная и горизонтальная линии проходят через соответствующие оси. Однако эти ограничения перекрываются тем, что требуется, чтобы Wa + Wb было меньше или равно единице. Чтобы понять расположение этого ограничения, допустим, что 100% инвестировано в А и ничего в В, тогда ограничение будет находиться в точке N. Если бы 100% было инвестировано в В и ничего в А, ограничение

максимизировать 0,03 и/ + 0,07%.

(9.14)

0,1 И/, + 0,3WU 0,2 0< Wa< 1 0< Wb<, 1 0 И/ + Wb< 1.

(9.15)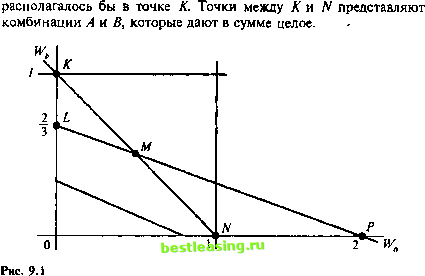

И наконец, существует ограничение 0,1 W, + 0,3W0,2. Для его иллюстрации мы проводим линию 0,1 Wa + 0,3 Wb = 0,2. Она представляет границу между областью точек, удовлетворяющих 0,1 Wa + 0,3Wb < 0,2, и областью, определяемой 0,1 Wa + 0,3 Wb > 0,2. Чтобы иметь правильное представление о расположении этой линии, предположим, что все инвестировано только в В и ничего в А. Мы должны были бы инвестировать лишь 2/3 наших денег, чтобы достичь дохода 0,2, потому что актив В приносит доход 0,3 на единицу (2/3 0,3 = 0,2). Если мы инвестируем только в актив А, нам необходимо вложить 200% наших средств, потому что по активу А зарабатывается лишь 0,1 (2 0,1 = 0,2).

Точки между А и М удовлетворяют ограничению Wa + Wb = 1, но не отвечают ограничению 0,1 Wa + 0,3 Wb й 0,2. Так же точки между М и Р соответствуют требованию 0,1 Wa + 0,3 Wb = 0,2, но не удовлетворяют ограничению Wa + Wb = 1. Таким образом, область возможных решений в этом примере должна быть ограничена линией 0LMN.

Теперь мы знаем, что оптимальная комбинация актива А и актива В лежит в пределах области 0LMN. Однако нам нужно знать, какая точка из этой области является оптимальной. Для этого обратимся к целевой функции 0,03 Wa + 0,07 Wb и постро-