чением Xj - собственным значением, таким, что когда диспери-онно-ковариационная матрица С умножается на вектор Xt, то это равно умножению вектора на скалярную величину X, т.е. СХ{ = XXj. Симметричность матрицы С означает, что существует и таких векторов (при условии, что С - это не единичная матрица, т.е. обладает обратной матрицей) и что они ортогональны (перпендекулярны друг другу).

Пример приведен ниже. Матрица 2 х 2 в левой части - это дисперсионно-ковариационная матрица, использованная ранее. Если эта матрица может быть помножена на вектор, так, что произведение будет равно произведению собственного вектора на скалярную величину, например:

0,00015 0,00005 0,00005 0,00025

Г т

является собственным вектором, то X - это соответствующее собственное значение.

Раскрыв скобки, мы получаем:

0,00015 + 0,00005m = X;

0,00005 + 0,00025m = Хт. (11.4)

Отсюда, умножая оба уравнения на т и сокращая X, мы получаем:

0,00015т + 0,00005/я2 = 0,00005 + 0,00025/и 0,00005/я2 - 0,00010т - 0,00005 = 0 5т2 - Ют - 5 = 0 т2 - 2т - 1 = 0

+ 2 ± V4 + 4 2± V8 гг

т =---= --- = 1 ± V2 .

Таким образом, собственные векторы равны:

(П.5)

Теперь мы должны нормализировать векторы так, чтобы длина их стала равна единице. Это значит, что каждая компо-

нента собственного вектора умножается на квадратный корень суммы квадратов каждой компоненты. Полученные нормализированные векторы являются собственными векторами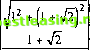

0,383 0,924

0,924 - 0,383

Запомним, что существует столько же собственных векторов, сколько переменных в дисперсионно-ковариационной матрице. Таким образом, в матрице 2x2 будут два собственных вектора, а в матрице п х п - п собственных векторов.

Мы можем доказать, что полученные векторы являются собственными векторами, потому что собственные векторы - это векторы, которые при умножении на матрицу С равны произведению вектора на скалярную величину. Например

0,00015 0,000050,383 0,00005 0,00025j[0,924

Здесь мы умножим матрицу С на вектор, чтобы получить новый вектор. Такой же вектор мы получим при умножении 0,000271 на первоначальный вектор. Таким образом, мы видим, что вектор в левой части - это собственный вектор, и скаляр 0,000271 - это собственное значение.

Точно такая же процедура применяется и к вектору в правой части, и в результате видим, что этот вектор также является собственным вектором

0,00015 0,00005] 0,924 0,00005 0,00025}- 0,383

0,000119 0,000050

0,000129

здесь собственное значение равно 0,000129.

0,924 - 0,383

Вторая стадия: построение матрии О. D и О-1

Следующий шаг - это построение трех матриц Q, D и Qrx. Матрицу Q строим из собственных векторов, записывая их как колонки матрицы в порядке убывания соответствующих им соб-

(116)

ственных значений. Таким образом, матрица Q для нашего примера будет

[ 0,383 0,9241 G~ [0,924 -0383J

Матрица D - это диагональная матрица (все значения, кроме значений на главной диагонали, равны нулю), значения на главной диагонали равны собственным значениям, в порядке убывания их значений. Таким образом, матрица D в нашем примере имеет следующий вид:

[0,000271 0

0 0,000129

(П.7)

Так, мы получим CQ = QD. Опять-таки при условии, что С и Q неединичные матрицы, мы сможем записать С = QDQ~l. Однако, если длина собственных векторов равна единице, т.е. сумма квадратов компонент собственных векторов равна единице, то матрицей, обратной Q, будет сама матрица Q, тогда можно записать, что С = QDQ.

С Q D Q~x

0,00015 0,00005 0,00005 0,00029

0,383 0,924 0,924 -0,383

0,000271 0,0

0,0 0,000129

0383 0,924 0,924 - 0,383

(11.8)

Третья стадия: определение линейных комбинаций переменных и ранжирование комбинации согласно их собственным значениям

Теперь рассмотрим дисперсионно-ковариационную матрицу С. Мы предположим, что она относится к двум активам X к Y. Дисперсия этого портфеля из двух активов может быть записана как

[X Y]

0,00015 0,00005

0,00005

0,00025

(П.9)

Но поскольку С = QDQ~l, она может быть записана как 0,383 0,924Т0,000271 0,0 ТО,383

[X Y]

0,924 - 0383j[0,0

0,00012910,924

0,924 - 0,383

±гУ

(11.10)