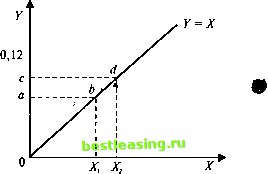Рис. 3.5

Затем рассмотрим прямоугольник QcdX2. Площадь опять будет X2, при X- Xi, площадь треугольника будет X1/!.

Теперь рассмотрим площадь многоугольника X\bdXi. Она равна разности площадей двух треугольников: ЫХ2-ЪЬХ\. Мы можем рассчитать площадь многоугольника, вычислив площадь каждого из треугольников и вычитая меньшую из большей. Однако существует более легкий способ, который также применим к случаям, когда график функции не является прямой. Этот способ использует концепцию первообразной, рассмотренную выше. Как уже выше сказано, график прямой линии описан функцией Y = X и независимо от значения X, площадь двух треугольников выражена функцией Х2/2. При этом Х2/2 является первообразной от X. Так как X - Xх, мы можем показать это следующим образом:

Х1+] X2

первообразная от X =-= -.

1 + 1 2

Таким образом, мы можем найти площадь под кривой между Х\ и Х2 путем нахождения первообразной от X, выразив первообразную в значениях Х\ и Х2 и затем вычитая из большего значения меньшее.

Указание на взятие интеграла с использованием первообразной функции J[X) обычно обозначается так:

J/(x)dJf = [F(X)fj , (3.64)

где j и к - нижнее и верхнее значения по X интегрируемой функции.

Сначала для X = 2 мы получим

Затем для Х= 4:

Отсюда площадь под кривой будет

8-2 = 6.

Мы можем проверить это, обратившись к рис. 3.5. Площадь греугольника OdXi при X = 4 будет 42/2 = 8. Площадь треугольника ОЬХ при JST = 2 будет 22/2 = 2.Вычитая из площади тре-дольника 0dX2 площадь треугольника 0ЬХ\, получим 8-2 = 6. Гот же самый результат получен при помощи первообразной.

Теперь рассмотрим другую линейную функцию, Y = 4Х, график которой изображен на рис. 3.6.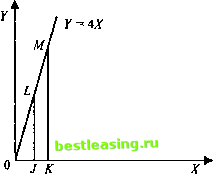

Рис. 3.6

Теперь предположим, что j = 2 и к = 4. Мы знаем, что первооб-азная от X - это X2/!. Отсюда для нахождения площади под кри-ой Y = Xмежду Х= 2 и К = 4 мы определим следующий опреде-енный интефал, подставляя значения Хв первообразную:

Нам надо найти площадь многоугольника JLMK. Для этого надо найти площади треугольников ОЫ и ОМК и вычесть первую из последней. Этот же результат достигается взятием определенного интеграла

4лг<иГ=(ЛГ)]} ,

где F - первообразная АХ.

Сначала возьмем первообразную от АХ, т.е.

первообразная от 4Х = --- = 2Х .

Чтобы определить площадь под кривой между J = 2 и К = 5, значения 2 и 5 подставляются в первообразную вместо X и вычисляется разница:

j4*cUf = [2*2] ,

что составляет

2(5)2 - 2(2)2 = 2 25 - 2 4 = 50 - 8 = 42.

Таким образом, площадь под кривой между X = 2 и X = 5 равна 42 квадратным единицам.

Это и есть применение основной теоремы математического анализа, которая гласит, что для определения площади под кривой Y=j(X) следует взять первообразную от функции / между точками j и к.

Приведенные выше примеры относятся к ситуации, когда Y - линейная функция от X и верхняя граница площади - прямая линия. Тем не менее аналогичный способ может быть использован для нахождения площади под кривой, где У является нелинейной функцией от X. Чтобы показать это, мы вновь прибегнем к использованию треугольников - см рис. 3.7.

Здесь мы опять хотим вычислить площадь под кривой между а и Ъ. Можно начать с построения множества прямоугольников с шириной АХ и высотой, равной расстоянию от оси ОХ до кривой в верхней границе АХ. Мы видим, что сумма площадей построенных прямоугольников больше площади под кривой из-за небольших участков, близких по форме к треугольникам, которые выступают над кривой. Заметьте также, что это указывает на ин-