будет нормально распределено вне зависимости от действительного распределения данных при условии конечной дисперсии.

Для демонстрации центральной предельной теоремы рассмотрим ежеминутные изменения индекса FTSE 100. Допустим, что в течение следующей минуты индекс либо возрастет, либо упадет на один пункт с одинаковой вероятностью. Эта вероятность описывается следующим образом:

Возможный результат -1 +1 Вероятность 0,5 0,5

В следующую минуту индекс может вырасти или упасть на один пункт с равной вероятностью, а потому возможные результаты в конце двухминутного периода будут определяться следующим образом:

Возможный результат -2 0 +2 Вероятность 0,25 0,5 0,25

За третью минуту индекс может измениться таким образом: если он был равен -2, то может возрасти до -1 или упасть до -3. Если он был равен 0, то может возрасти до + 1 или упасть до -1. Если же индекс был равен + 2, то может стать + 3 или + 1. Возможные результаты будут такими:

Возможный результат -3 -1 +1 +3 Вероятность 1/8 3/8 3/8 1/8

Через четыре минуты результаты будут следующими:

Возможный результат -4 -2 0+2+4 Вероятность 1/16 1/4 3/8 1/4 1/16

Можно увидеть, что уже после четырехминутных интервалов вероятность получения крайних результатов, например, -4 или + 4, становится довольно низкой, а вероятность получения результата, близкого к математическому ожиданию, сравнительно высока. Если бы мы продолжили процесс еще на некоторый промежуток времени, то увидели бы, что функция вероятности принимает колоколообразную форму нормального распределения.

Заметьте, что приведенный выше пример всего лишь описывает тенденцию собранных данных. Центральный предельный процесс описывает поведение средних собранных данных.

Стандартизованная Функция плотности вероятностей нормальной кривой

Стандартизованная (или нормированная) переменная, обычно обозначаемая Z, - это переменная со средней арифметической, равной нулю, и средним квадратическим отклонением, равным единице, вычисляется по следующей формуле:

Если случайная переменная нормально распределена, то стандартизованная переменная z будет нормально распределена с математическим ожиданием, равным нулю, и средним квадра-тическим отклонением 1,0. Поскольку нормальное распределение - это распределение вероятностей, то площадь под кривой должна быть равна I. Кривая изображена на рис. 4.4.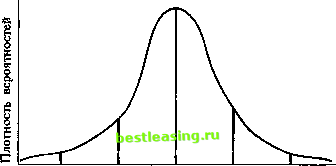

-3 -2 -1 0 +1 +2 +3

Рис. 4.4

Высота от любой точки кривой до оси абсцисс представляет собой функцию плотности стандартизованной кривой нормального распределения. Уравнение функции плотности стандартизованного нормального распределения выглядит следующим образом:

(4.27)

Зависимость между стандартизованной и не стандартизованной функциями плотности нормальной кривой, данной в уравнении (4.25), становится очевидной.

Площадь любого вертикального сегмента под кривой представляет вероятность того, что нормально распределенная случайная переменная примет значение на интервале, ограниченном данным сегментом. Это показано на рис. 4.5.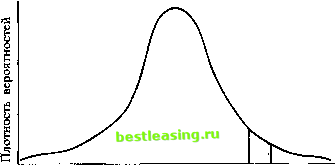

1,0 1,5

Рис. 4.5

Нахождение плошадей

под кривой нормального распределения

с помощью таблии

В таблицах приведены площади под стандартной кривой нормального распределения так называемого стандартизованного нормального распределения. Обычно в таблице при помощи диаграммы указывается, площадь каких сегментов приводится. Но при отсутствии диаграммы, взглянув на данные, приведенные в таблице, можно легко увидеть, приведены ли в таблице площади справа или слева от X для различных значений. Обычно таблицы содержат площади сегментов под кривой справа от X для значений X больше нуля. Прочие площади можно вывести, используя симметричность кривой. Площади (т.е. веро- * ятности) могут быть найдены как разность двух табличных величин для 1= а и для X = Ъ.

Для определения вероятности того, что нормально распределенная переменная примет значение в пределах какого-либо обусловленного интервала, во-первых, надо найти значение z для верхней и нижней границ интервала.