правой части уравнения будет нормально распределена, и соответственно ln(i5y S/-i) будет тоже нормально распределено.

Переменная называется логнормально распределенной, если натуральный логарифм ее нормально распределен. Следовательно, если \n(Sl+itt/S(f)) нормально распределен, то St+it/S должно быть распределено логнормально.

Это очень привлекательная модель распределения отношений цен ценных бумаг, потому что, если цена растет, то отношение цен будет больше единицы, если падает - то отношение цен будет меньше единицы, но оно никогда не принимает отрицательного значения. Теперь рассмотрим график функции логнормаль-ного распределения на рис. 4.7. На рисунке видно, что логнормальное распределение вытянуто вправо, но не имеет отрицательных значений. Это совместимо с возможным распределением цен ценных бумаг, поскольку они не могут упасть ниже нуля, и только очень немногие из наблюдений могли быть очень высоки.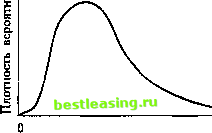

Рис. 4.7

Переменная не может принимать отрицательные значения, и вероятность очень высоких значений приближается к нулю, как это и можно ожидать от переменной, описывающей относительное изменение цены ценной бумаги. Логнормальное распределение очень часто используется для моделирования такого рода случайных переменных, в основе которых лежит процесс умножения.

Мы отметили в гл. 1, что натуральный логарифм относительной цены ln(St/St i) - это непрерывно начисляемая доходность

ценной бумаги S за период времени t- (t- 1). Если относительные цены логнормально распределены, непрерывно начисляемая доходность ln(St/St-i) будет также логнормально распределена.

К этому распределению мы вернемся в гл. 10, где используем его для оценки опционов. Следующие результаты доказаны в приложении к этой главе. Если- *

Ыг)~ЛГ(ц,о-2), (4.31)

Дг) =еМ+ 2 . (4.32) Для удобства это часто записывается так:

ехр(ц + о72); (4.33)

var( Y) = е2**+°2 (е°2 -1). (4.34)

Биномиальное распределение

Одним их наиболее важных дискретных распределений в финансах является биномиальное распределение. Для формирования биномиального распределения случайная переменная должна отвечать следующим четырем условиям.

1. Переменная может принимать только два значения в данный момент или в результате данного события. Каждое из этих событий или моментов времени называется биномиальной попыткой. Два возможных результата называются успех - в случае благоприятного результата и неудача - в случае неблагоприятного.

2. Для каждой последовательности попыток вероятность успеха и неудачи постоянна.

3. Все попытки идентичны.

4. Все попытки независимы.

Биномиальная случайная переменная X - это число успехов в результате некоторого количества независимых попыток п. Результат испытания записывается как успех или неудача, и вероятность успеха в каждой из попыток равна р. Мы говорим АЧжном (я, р). X, число успехов в я попытках, может принимать значения 0, 1, 2, я. Таким образом, для я попыток может быть я + 1 результат. Один

результат будет включать я успехов, другой - я-1 успехов, и т.д. и последний - вообще без успехов.

Это показано на рис. 4.8, где переменная S может возрастать в и раз (м >1) или уменьшаться в d раз (0 < d < 1). В данном случае мы имеем две биномиальные попытки и три результата. Результат Su2 - это результат двух успехов, т.е. j = 2. Результат Sud = Sdu, т.е. j = 1 - это результат одного успеха. И результат Sd2 - это результат нулевого количества успехов, т.е. j = 0.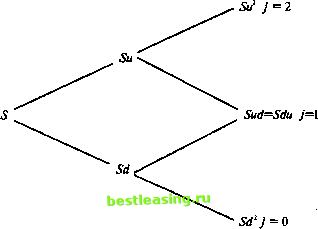

Рис. 4.8

Биномиальное распределение дает вероятности X для каждого из результатов. Вероятность достижения каждого из них зависит от:

1) вероятности успеха, т.е. р;

2) общего числа способов достижения результата.

Чтобы объяснить вероятности, связанные с этим деревом , рассмотрим вероятность получения двух последовательных успехов. Предположим, что вероятность успеха равна 0,5 и, учитывая, что попытки независимы, вероятность двух успехов PiSu2) будет равна 0,5 0,5 = 0,25. Таким же образом вероятность, успеха, следующего за неудачей, также будет 0,25.

Вероятность успеха, следующего за неудачей, равна вероятности неудачи, следующей за успехом. Отсюда существует два