способа достижения одного успеха. Каждый способ имеет вероятность 0,25, и значит, вероятность результата у = 1 будет 0,25 + + 0,25 = 0,5.

Для нахождения вероятности в более сложных примерах, например, если вероятности роста и падения не равны или очень много попыток, необходима Азнать количество результатов, имеющих определенное число успехов. В рассматриваемом примере мы хотим узнать, сколько результатов соответствуют одному успеху, сколько - двум и сколько - нулю. Можно рассчитать число у - количество успехов для заданного числа я биномиальных попыток, используя формулу:

Cj = . й! (4.35)

где Cj - количество способов достижения у успехов из я попыток;

и - число биномиальных попыток; у - число успехов.

Знак ! после я и у обозначает факториал, т.е. п умножаем на (и - 1) (я-2) (я - 3) и т.д. Например, для я = 4 найдем я!

4 3 2 1 = 24,

у! рассчитывается подобным же образом.

Для демонстрации использования формулы (4.35) определим число способов получения одного успеха в данном примере:

2! 2-1 2 1!(2-1)! 11

Этот результат можно легко проверить. В рассматриваемом примере Sud и Sdu приводят к одному успеху каждый.

Теперь, зная число результатов с у успехами, определим вероятность получения у успехов с л попыток, поскольку это даст нам вероятность, связанную с количеством результатов, имеющих у успехов. Эта вероятность находится по формуле

p{x = j) = jKn-jy.pJ(l~p)(, J) (4,36)

где р - вероятность успеха и 1-р - вероятность неудачи.

Для примера вспомним, что мы предположили, что р = 0,5 и (1 - р) = 0,5. Вероятность конкретного результата (Su2) после двух попыток отсюда равна:

piSu2)= 2\(2-2)!0,52(1 -05)(2 2) =о,25 = ОД5.

Таким образом, существует всего лишь один результат cj=2 числом успехов, и он имеет вероятность 0,25. Теперь рассчитаем вероятности Sud и Sd2 Для Sud

P(Sud) = vJ[lv0f (1 - О.б)2 1 = 0,5.

Существуют два результата, дающих j = 1 успеху, каждый имеет вероятность 0,25. Два таких результата имеют вероятность 0,5. Для Sd2

Р(Ы2) = -05° (1-05)V-V =0,25. 0!(я-0)!

Складывая все полученные вероятности, получаем единицу, как и следовало ожидать.

Математическое ожидание, дисперсия и среднее квадратическое отклонение распределения составят:

Е(Х) = пр; Var(A) = пр(\-р);

SD(X)=J(np(l-p)) .

В случае же большого числа наблюдений биномиальной случайной переменной, где значение математического ожидания не приближается ни к нулю, ни к п, распределение вероятностей приближается к нормальному распределению со средней и дисперсией, соответственно равными

Е(х) = пр;

о\=пр(\-р). (4.37)

Биномиальное пепево иен активов

Наиболее частое применение биномиального распределения в финансах - это в отношении изменений цен ценных бумаг, где допускается, что в течение следующего малого промежутка времени цена может либо возрасти ( успех ), либо упасть ( неудача )

на определенную величину. Биномиальная модель используется как допущение при определении цены опционов. Расчет ожидаемого значения цены актива с применением биномиальной модели состоит из трех шагов: создание биномиального дерева возможных цен активов; определение вероятностей каждого из возможных результатов; умножение каждого из возможных результатов на его вероятность. Сумма произведений и составит ожидаемое значение.

Например, рассмотрим случай, когда надо найти значение цены актива по истечении двух временных интервалов, т.е. после двух биномиальных попыток. Допустим, что в результате каждой попытки существует вероятность роста цены, равная 0,5 (т.е. р = 0,5), либо падения, равная 0,5 (1-р = 0,5). Допустим также, что изменение цены в один период времени не зависит от изменения цены в другой период. На рис. 4.9 возможные изменения цены изображены в виде биномиального дерева.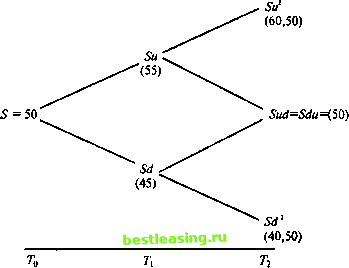

Рис. 4.9

Обозначим настоящий момент времени 7Ь, конец первого интервала - Т\, цена актива с равной вероятностью либо возрастает до Su, либо падает до Sd. К концу второго промежутка времени Тг, если цена к тому моменту была Su, то она может