Для демонстрации этого мы можем подсчитать, что если X подчиняется распределению Пуассона, вероятность того, что X находится в интервале от 25 до 30 включительно, будет 0,391 (с точностью до трех знаков после запятой).

Записываем Д25 £ Х< 30) = 0,391.

Теперь приближаем X посредством Y- N(30, 30).

Для проверки приближения находим Д24,5 < Y < 30,5). Здесь 0,5 представляет собой поправку на непрерывность, поскольку дискретная величина 25 на распределении Пуассона аппроксимирована интервалом 24,5 - 25,5 на непрерывной кривой нормального распределения

где z~ N(0, 1).

Приближение будет лучше при больших X, когда оно действительно требуется.

Таким образом, мы видим, что распределение Пуассона применимо в условиях, сходных с условиями для биномиального, за исключением тех случаев, когда число j очень мало, а число попыток п велико. Сейчас мы рассмотрим использование распределения Пуассона на примере больших скачков значения индекса FTSE 100.

Предположим, что нужно смоделировать процесс ежедневного изменения индекса FTSE 100 на более чем 1%. Можно представить, что за определенный период эти изменения случайны, но происходят, скажем, раз в месяц, т.е. 12 раз в год. Как много изменений можно ожидать в течение следующих шести месяцев? Очевидно, мы ожидаем шесть изменений, но мы не очень удивимся, если произойдет четыре, пять, восемь, или любое другое число изменений, близкое к шести.

С первой попытки мы можем построить модель, разбив эти месячные периоды на недельные подпериоды. Затем мы представляем такое изменение происходящим или не происходящим в каждом интервале с вероятностью 12/52, где 52 - число недель в году. Предположив, что данные события должны быть независимы, мы получаем бином с параметрами (26, 12/52). Хотя это и неплохая отправная точка, но это биномиальное распределение является неадекватной моделью практической ситуации, поскольку допускается либо отсутствие изменений, либо одно из-

/>=(24,5<Г<30,5)=/>

24,5-30 , л/30

= /41,00 < z < 0,09) = 0377 ,

(4.39)

менение в течение каждого недельного подпериода. Можно разбить; недельные интервалы на дни и использовать биномиальное распределение с параметрами (183, 12/365), но, как мы уже отметили, гораздо эффективнее предположить, что наша случайная переменная подчиняется распределению Пуассона.

Распределение Пуассона описывается следующим образом:

Р(Х = г) = -f -. (4.40)

Продемонстрируем использование распределения Пуассона, вычислив вероятность того, что в течение следующих шести месяцев произойдет больше трех скачков индекса, превышающих 1%.

Анализ информации об индексе FTSE 100 с 3/1/84 по 3/4/92 показывает, что на протяжении 8,25 лет среднее число ежедневных изменений индекса более, чем на 1%, за каждый шестимесячный период, составило 5.

Вероятность наступления одного изменения будет равна:

е-55

/>(j = l) = £ i = 0,0337.

Чтобы найти вероятность по крайней мере трех таких изменений в течение следующих шести месяцев, следует найти вероятности Х= 0, Х= 1и Х= 2, сложить их и вычесть из единицы. Получаем:

Р(Х = 0) = = 0,0067 ;

Р(Х = = = 0,0337; />(* = 2) = ill! = 0,0842.

Таким образом,

P (X* 3) = (Х= 0) + Р(Х= 1) + Р(Х= 2)) =

= 1 - 0,1246 = 0,875.

Следовательно, существует вероятность, равная 87,5%, что произойдет по крайней мере три дневных изменения индекса FTSE 100 на 1% и более в течение следующих шести месяцев.

Распределение Парето-Леви

Нормальное распределение не является панацеей для всех проблем при моделировании. В частности, его использование при моделировании относительных цен активов может быть подвергнуто сомнению по крайней м>ере по двум причинам:

1) предполагается, что относительные цены независимы с течением времени, в то время как они демонстрируют автокорреляцию;

2) вероятность наступления крайних событий в действительности выше, чем это подразумевается нормальным распределением.

Эти факторы указывают на потребность в распределении, которое после логарифмической трансформации будет иметь более высокий пик (как следствие автокорреляции) и более жирные хвосты (вследствие частоты крайних значений).

Определенно такие симметричные распределения должны иметь коэффициент эксцесса больше нуля (для нормального распределения он равен нулю). Распределения с коэффициентом больше нуля называются островершинными (leptokurtic) (см. рис. 4.10), распределения с коэффициентом эксцесса меньше нуля называются плосковершинными (platykurtic).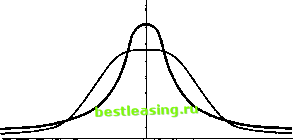

Рис. 4.10

В то время как упомянутые выше распределения определены на основе реальных обстоятельств, в соответствии с которыми они подбираются, было бы полезно иметь теоретическое распределение, наиболее полно соответствующее наблюдаемым явлениям, даже если между ними нет никакой очевидной физической связи. В таких обстоятельствах особенно полезны се-