Прежде чем перейти к рассмотрению других значений г\ из (40:3), заметим, что выводы (40:В) и (40:С), очевидно, представляют собой прос-стейшие примеры общего метода определения игр. Эта процедура (более общая, чем в главе X, на которую была ссылка в замечании на стр. 313) будет исчерпывающим образом рассмотрена в другом месте (в том числе и для асимметричных игр). Она подчинена некоторым ограничениям арифметической природы; таким образом ясно, что не может быть (существенных, симметричных, с нулевой суммой) игр п лиц, в которых любая коалиция из р лиц выигрывает, если р является делителем п, так как в противном случае могут образоваться nip таких коалиций, каждая из которых выигрывает, и не остается проигрывающих игроков. С другой стороны, то же самое требование при р = п - 1 вообще не накладывает ограничений на игру (см. сноску 3, стр. 347).

40.3. Связь между симметричной игрой пяти лиц и 1,2,3-симметричными играми четырех лиц

40.3.1. Рассмотрим теперь значение г), расположенное внутри интервала (40:3). Эта ситуация в некотором роде аналогична ситуации, рассмотренной в конце п. 35.3. У нас имеются некоторые эвристические соображения относительно условий на обоих концах (40:3) (см. выше). Любая точка г) из (40:3) в некотором смысле окружена этими концевыми точками. Точнее говоря, она является их центром тяжести при подходящих весах этих точек х). Замечания, сделанные выше, применяются снова: хотя это построение описывает все игры (40:3) в виде комбинаций крайних случаев (40:В), (40:С), тем не менее неизвестно, могут ли быть стратегии исходной игры получены непосредственно из стратегий крайних игр. Наш опыт в случае игры четырех лиц с нулевой суммой говорит сам за себя.

Имеется, однако, и другая аналогия с играми четырех лиц, дающая некоторые эвристические соображения. Число параметров в нашем случае такое же, как для игр четырех лиц с нулевой суммой, симметричных относительно игроков 1, 2, 3; мы теперь имеем единственный параметр г, пробегающий интервал

(40:3) -4т!2,

а упомянутые игры имели параметр хи изменяющийся в (40:4) - 1х,12).

Эта аналогия между полностью симметричной игрой пяти лиц и 1, 2, 3-симметричной игрой четырех лиц пока чисто формальная. Однако в ней скрывается более глубокий смысл. Чтобы увидеть это, поступим следующим образом.

40.3.2. Рассмотрим симметричную игру пяти лиц, где ц принадлежит интервалу (40:3). Модифицируем теперь эту игру, объединяя игроков 4 и 5 в одно лицо, т. е. в игрока 4. Обозначим новую игру через Г. Важно понять, что Г - совершенно новая игра: мы не утверждали, что в Г игроки 4 и 5 будут обязательно действовать совместно, т. е. составят коалицию, и т. п., или что имеются какие-то общие стратегические при-

1) Читатель легко сможет вывести это представление в смысле замечания на стр. 319 с помощью наших уравнений (40:1), (40:2) в п. 40.1.2.

2) См. п. 35.3.2. В представлении на кубе Q, использованного там, xt = х2 = х3.

чины, которые мотивировали образование именно такой коалиции 1). Мы заставили игроков 4 и 5 объединиться; мы сделали это в результате изменения правил игры и тем самым заменой игры Г на игру Г.

Итак, Г - это симметричная игра пяти лиц, а Г - 1,2, 3-симметрич-ная игра четырех лиц 2). По данному г) для Г мы хотим определить хх для Г, для того, чтобы определить соответствие между (40:3) и (40:4). Затем мы будем исследовать, существуют ли, несмотря на все сказанное, какие-либо связи между стратегиями, т. е. между решениями игр Г и Г.

Характеристическая функция v (S) игры Г выражается непосредственно через характеристическую функцию v (S) игры Г. В самом деле:

v ((1)) = v ((1)) = -1, v ((2)) = v ((2)) = - 1,

v ((3)) = v ((3)) = -1, v ((4)) = v ((4, 5)) = - т

v((l, 2)) = v((l, 2))= -т, v((l, 3)) = v((l, 3))= т),

v((2, 3)) = v((2, 3))=-ть v((l, 4)) = v((l, 4, 5)) = t

v ((2, 4)) = v ((2, 4, 5)) = n, v ((3, 4)) = v (3, 4, 5)) -= tj,

v((l, 2, 3)) = v((l, 2, 3)) = r, v((l, 2, 4)) = v((l, 2, 4,5)) = 1,

3. 4)) = v((l, 3, 4, 5)) = 1, v((2, 3, 4)) = v((2, 3, 4, 5))=1

и, разумеется,

v(0) = v ((l, 2, 3, 4)) = 0.

В то время как игра Г была нормирована и редуцирована, игра Г не является таковой, и мы должны привести ее к такой форме, так как мы хотим вычислить для нее параметры х±, х2, х3, т. е. найти ее местоположение в кубе Q из п. 34.2.2.

Поэтому применим сначала формулы редуцирования из п. 27.1.4. Они показывают, что выигрыш игрока к - 1, 2, 3, 4 должен быть заменен величиной al, где

X = - V ((*)) + 4- К ((1)) + V ((2)) + v ((3)) + v ((4))}.

V = -т {V ((1)) + V ((2)) + v ((3)) + v ((4))}.

Следовательно,

< + < + < =

3(1-Л) 3 + г]

з-i-

2 5

Ясно, что здесь 7 -- = > 0 по (40:3); следовательно, игра является существенной. Нормировка осуществляется теперь делением доли каждого игрока на 7.

*) Это должно контрастировать с рассуждениями п. 36.1.2, где аналогичная комбинация двух игроков была составлена при таких условиях, что это объединение казалось стратегически оправданным.

2) Участники игры Г - это игроки 1, 2, 3, 4, 5, все равноправные в исходной игре Г. Участники игры Г - это игроки 1, 2, 3 и составной игрок (4, 5), т. е. игрок 4. Ясно, что 1, 2, 3 играют свою прежнюю роль, а 4 - другую.

Таким образом, для двухэлементного множества S = (t, 7) v (S) заменяется на

V (S):

V (5) + о? + а

Теперь простое вычисление дает нам

v ((l, 2)) = v ((l, 3)) = V((2, 3)) =

v ((l, 4)) = v ((2, 4)) = v ((3, 4)):

2(3ti-1) 3 + t)

2(3ii-l)

Эта характеристическая функция является нормированной и редуцированной формой, которая использовалась в п. 34.2 для представления в кубе Q. Равенства (34:2) из п. 34.2.1 вместе с приведенным выше выражением дают формулу х4 = х2 = xs - . При х1 = х2 = х3 это соотпо-шение можно также переписать в виде

(40:5)

(3-*,) (3 + л) = 10.

Теперь легко проверить, что (40:5) отображает т)-область (40:3) на ггобласть (40:4). Это отображение, очевидно, монотонно. Все подробности: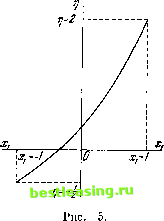

1 2 5

77: -- - L JL I 2 7 S 3 13

А ±

13 7

i 1

~ 1

-> gL 1

5 9 3

! А

! в\с\ в

2 ив 343 4 Рис. 46.

видны из рис. 45 и из таблицы соответствующих значений х{ и ц на рис. 46. Кривая на рис. 45 отвечает соотношению (40:5) в плоскости хи т). Ясног что эта кривая является гиперболой (ее дугой).

40.3.3. Наш анализ 1-, 2-, 3-симметричных игр четырех лиц завершился результатом, зафиксированным в п. 36.3.2: такие игры, т. е. диагональ /-центр-У/7/ в Q, представляющая их, делятся на пять классов А - Е, каждый из которых характеризуется определенным качественным типом решений. Расположение зон А - Е на диагонали /-центр-F /, т. е. на интервале - 1 :g х{ 5g 1, показано на рис. 44.

Полученные результаты наводят поэтому на мысль о рассмотрении соответствующих классов симметричных игр пяти лиц Г в надежде, что из сравнения каждого класса с классом 1,2,3-симметричных игр четырех лиц Г появятся некоторые эвристические соображения о нахождении их решений.