нормальная зона -3 :g е0 :g 3/2, но теперь мы предпочитаем рассматривать все значения е0.

Это исследование будет проводиться графическим методом, который мы использовали при изложении старой теории в § 32. Поэтому мы будем следовать схеме § 32 в нескольких отнощениях.

Характеристическая функция здесь та же самая что и в п. 32.1.1:

С О (О

-1 1

(47:1) \(S)=\ если S имеет элементов

{ о U

Обобщенный дележ есть вектор

а = {а4, а2, а3},

три компоненты которого должны удовлетворять условиям (44:13) из п. 44.7.2, которые теперь принимают вид

(47:2) оц-1, а2 -1, а3 - 1.

Кроме того, согласно (44:11*) из п. 44.7.2 в Е (е0) избыток должен быть равен е0, и это условие теперь принимает вид

(47:3) а4 + а2 + а3 = е0 *).

47.2.2. Мы хотим представить графически эти дележи с помощью приема, описанного в п. 32.1.2. Но этот прием позволяет изобразить только такие тройки чисел, сумма которых равна нулю. Поэтому положим

(47:4) асц -ef, а2-а2---, а* = а3--.

Тогда условия (47:2) и (47:3) принимают вид

(47:2*) a-(l+), a2-(l+-), a3-(l+),

(47:3*) o + o + aO2).

Теперь становится возможным представление п. 32.1.2, причем нам нужно только заменить а4, а2, а3 на а1, а2, а3. С учетом этой оговорки можно использовать рис. 31.

По этим причинам для каждого вектора a = {a4, a2, a3} из E (e0) мы образуем не только его компоненты в первоначальном смысле, но также его квазикомпоненты а1, а2, а3, определенные равенствами (47:4), и с помощью этих квазикомпонент мы используем графическое представление рис. 31.

Итак, это представление на плоскости выражает в точности условие (46:3 *). Остальные условия (47:2 *) поэтому эквивалентны ограничению, на-

ложенному на точку а в плоскости на рис. 31. Это ограничение получается

х) Читатель должен сравнить условия (47:1) - (47:3) с условиями (32:1) - (32:3) из п. 32.1.1; единственное отличие состоит здесь в равенстве (47:3).

2) При сравнении этих условий (47:2*) и (47:3*) с условиями (32:2) и (32:3) из п. 32.1.1 видно, что условия (47:3*) и (32:3) совпадают, а условия (47:2*) и (32:2) отличаются только коэффициентом пропорциональности 1 + .

таким же образом, что и аналогичное ограничение в п. 32.1.2: точка а должна лежать внутри треугольника, образованного тремя прямыми

1 (1 + а2 = - (1 + Ч), а3 = - (1 + Это есть в точности

-(! + =§), а =-(1+2).

ситуация рис. 32, за исключением наличия множителя пропорциональности 1 -f- е-~ и она изображена на рис. 49. Заштрихованная область, которая будет называться фундаментальным треугольником представляет дележи а, удовлетворяющие условиям (47 : 2*) (47 : 3*), т. е. принадлежащие Е (е0).

47.2.3. В этом графическом представлении мы выразим отношение доминирования. Так как мы используем новую теорию, рассуждения

п. 31.1 относительно множества S

для отношения доминирования а е- р, т. е. рассуждения относительно того, является оно заведомо необходимым или заведомо не необходимым, больше неприменимы. Поэтому мы изучим множество S заново.

По-прежнему справедливо, что S не может состоять из одного или из трех элементов. В первом случае S = (£), так что согласно п. 30.1.1, ccf v ((*)) = -1, at > pf и, следовательно, Pj < -1, что противоречит неравенству Pi -1 ввиду (47:2). Во втором случае S = (1, 2.J3), так что согласно п. 30.1.1 а4 > Pi, <*2 > Рг> > Рз и, следовательно, i + 2 + з > Pi + Р2 + Рз> что противоречит равенству а4 + а2 + + а3 = Pi+ Р2 + Рз = е0 ввиду (47.3).

Таким образом, множество S должно состоять из двух элементов, S = (£, ;) 2). Тогда доминирование означает, что аг -f <х7- 5g v ((£, 7)) = 1 и г> Рп у > ру, т.е.

и а*>р\ aJ>p3. Ввиду (47:3*) первое условие моягао записать в виде Таким образом, мы установили следующее: отношение доминирования

р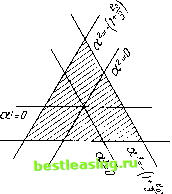

Рис. 49.

х) См. сноску 2 на стр. 417. Здесь мы, конечно, предполагаем, что 1 + -0,

Если 1 + < 0, т. е. е0 < - 3 = - Г 14, то условия (47.2*), (47:3*) несовместны,

и действительно, как мы знаем из (45:А), в этом случае множество Е (е0) пусто. 2) f, /, к есть перестановка 1, 2, 3.

означает, что

(47:5)

либо сХЗ1, а2>р2 иа3>-(1-) , либо а11, а3>р3 и а2-(lД°) , [либо а2>р2, а3>р3 и а1-(l--)

47.3. Рассмотрение шести случаев. Случаи (I) - (III)

47.3.1. После этих предварительных замечаний мы можем перейти к рассмотрению решений V игры Г для Е (е0) для всех значений е0.

Окажется удобным различать шесть случаев. Из этих случаев случай (I) соответствует (45:0:а), случаи (II) - (IV) и одна часть из случая (V) - (45.0:Ь) (нормальной зоне), а случаи (V) и (VI) (исключая эту часть) - (45:0:с) (все в п. 45.6.1).

47.3.2. Случай (I): е0 < - 3. В этом случае 1 + е-~ < 0, так что

условия (47:2*) и (47 : 3*) несовместны, и Е (е0) пусто (см. сноску 1 на стр. 418); следовательно, множество V также должно быть пустым.

Случай (II): е0 = -3. В этом случае 1 + = 0 и из (47 : 2*) и

(47 : 3*) следует, что а1 = а2 = а3 = 0, т. е. at = а2 = а3 = е0/3 = -1,

а = { - 1, -1, -1}. Таким образом, Е (е0) состоит из одного элемента, и должно быть V = Е (е0) ввиду тех же рассуждений, которые использовались при доказательстве (31:0) из п. 31.2.3. Таким образом, эта ситуация очень похожа на ту, которая встретилась в несущественной игре (см. соответствующее место).

Случай (III): -3 < е0 0. В этом случае 1 + > 0, так что мы можем использовать рис. 49. Кроме того, 1 + ~ :g 1 - так что

дополнительные условия (47:5) из п. 47.2.3 автоматически выполнены во всем фундаментальном треугольнике. Итак, (47:5) совпадает с (32:4) из п. 32.1.3 (см. сноску на этой стр.). Следовательно, снова применимы все рассуждения пп. 32.1.3-32.2.3, если ввести множитель пропорциональности 1 + ~.

Таким образом, в этом случае мы получаем решения для Е (е0) простым умножением на 1 + каждой компоненты описанного в п. 32.2.3 решения и прибавлением к результату £0/3 (для перехода от а1 к аг).

х) Эти условия отличаются от соответствующих условий (32:4) из п. 32.1.3 только дополнительным неравенством в конце каждой строки.

47.4. Случай (IV). Первая часть

47.4.1е. Случай (IV): 0 < е0 < 3/2. В этом случае 0 < 1 - < 1 -f

-f -~. Следовательно, прямые