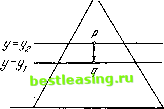Прямая I

Рис. 59.

заштрихованного в клеточку. Сравнение рис. 58 с рис. 56 показывает, что эта точка г доминирует как р, так и q. Так как р, q £ V, г не может принадлежать V. Следовательно, в V должна существовать точка s, которая доминирует г. Повторное сравнение рис. 58 с рис. 56 показывает, что точка, которая доминирует г, должна также доминировать либо р, либо q. Так как все точки s, р, q принадлежат V, это невозможно.

47.5.4. Предположим теперь, что yt (в треугольнике Г, т. е. между основанием I и вершиной о) не есть ордината какой-либо точки, принадлежащей V. Тогда наверняка существуют точки из V с ординатами у Уи например, такой точкой является вершина о. Выберем из V /Точкао точку р с ординатой у г/4 и расположенную возможно ниже, т. е. точку с минимальной ординатой у *) (рис. 59). Обозначим это минимальное значение через у = у2- Ясно, что У\<Уъ- По определению у2 никакая точка из V не имеет ординаты у, для которой i/i У <L Уг-> и согласно приведенным выше рассуждениям, р есть единственная точка из V с ординатой у = у2.

Спроектируем теперь точку р по вертикали на прямую у = у и мы получим точку q. Точка q не может принадлежать V, и, следовательно, она доминируется некоторой точкой s £ V. Поэтому эта точка s не может находиться ниже q, т. е. ее ордината у 7 yt. Следовательно, у у2.

Сравнение \ рис. 59 с рис. 56 Точна о показывает, что р не доминиру-

ет q. Следовательно, s Ф р, откуда необходимо следует, что У ФУ2- Таким образом, у>у2, т. е. s находится определенно выше р. Повторное сравнение рис. 59 [с рис. 56 показывает, что если точка s, лежащая выше р, доминирует точку q, то она должна также доминировать р. Так как обе точки р принадлежат V, это невозможно.

47.5.5. Подведем итоги: каждое у (между I и о) есть ордината в точности одной/точки из V. Если у изменяется, то эта точка изменяется так, что сохраняются ограничения рис. 57, т. е. она изменяется в заштрихованных областях, указанных на этом чертеже. Другими словами:

{47:6) V (в Т) представляет собой кривую, идущую от вершины о

до основания Z, направление которой никогда не отклоняется от вертикали более чем на 30° 2) (см. рис. 60).

х) Это возможно, так как V есть замкнутое множество; см. утверждение (*) замечания на стр. 397.

2) Следовательно, она непрерывна.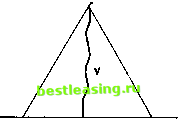

Прямая I

Рис. 60.

Обратно, если дана произвольная кривая, удовлетворяющая (47:6), то из сравнения рис. 60 с рис. 56 становится ясно, что области, доминируемые точками из V, составляют в точности дополнение V в Г. Таким образом, (47:6) есть точное определение части V в Т *).

Теперь мы можем получить общее решение V для Е (е0) (т. е. для фундаментального треугольника), проводя в каждом заштрихованном

треугольнике на рис. 53 и 54 кривые, соответствующие рис. 60. Результаты изображены соответственно на рис. 61 и 62 2).

Нужно отметить, что эти рисунки все еще имеют заметное сходство с рисунками, описывающими решения существенной игры трех лиц в старой теории (см. п. 32.2.3, что видно на внутреннем треугольнике на рис. 52). Новое представляют собой кривые в малых треугольниках, каждая из которых расположена в полосе между двумя главными треугольниками рис. 61 и 62. Ширина этой полосы, как показано на рис. 50 и следующих, измеряется числом e0s). Поэтому, когда е0 стремится к нулю, новые решения приближаются к старым.

Следует также указать, что множество решений теперь гораздо разнообразнее, чем было раньше: можно выбирать произвольно целые кривые (соблюдая ограничения (47:6)). Далее мы увидим, что эти кривые наводят на мысль об одной интерпретации, имеющей дополнительное значение. (См. п. 47.8.)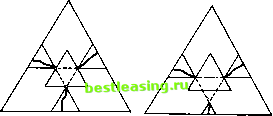

Рис. 61.

Рис. 62.

47.6, Случай (V) 47.6.1. Случай (V): 3/2 <; е0 < 3. В этом случае

1 0<1+-

*(i-*)<*+-J-)-

Как легко проверить, эти неравенства выражают тот факт, что ориентация внутреннего треугольника из рис. 50 противоположна ориентации внешнего (фундаментального) треугольника, но внутренний треугольник все еще расположен целиком внутри внешнего, как показано на рис. 63. Внешний треугольник снова разбивается на семь областей, каждую из которых можно охарактеризовать теми двухэлементными множествами, которые эффективны в ней в смысле (47:5) из п. 47.2.3. Единственное отличие между рассматриваемым случаем и случаем (IV) (т. е. рис. 50) состоит в поведении области 1. Список областей и соответствующих им эффективных множеств приведен ниже в таблице 26 к рис. 64.

х) Это также верно в случае, когда Т вырождается в точку; см. сноску 1 на стр. 421.

2) Нижний треугольник на рис. 62 может выродиться в точку или даже исчезнуть совсем; см. сноску 1 на стр. 421.

3) Стороны внешнего (фундаментального) треугольника задаются уравнениями

а1 = - ( з ) стороны внутреннего треугольника - уравнениями а1 =

= - 1 - ~ j (см. рис. 50). Разность чисел - 1 + -j и - 1 - ~ j равна

Теперь мы можем вычертить аналоги рис. 33 и 51, показывающие для каждой точки фундаментального треугольника заштрихованные области *), которые она доминирует. Это сделано на рис. 64 (см. табл. 26) в соответствии с (47:5).

Из рис. 64 ясно, что никакая точка области 1 2) не доминируется никакой точкой3). Следовательно, решение V должно содержать всю область 1.

47.6.2. Теперь, когда найдена часть V, содержащаяся в области 2, перейдем к определению остальной части V. Так как V есть решение, эта остальная часть V должна содержаться в области, которая не доминируется уже известной частью V, т. е. областью 1. Рассмотрение рис. 64 показывает, что эта недоминируемая область состоит в точности из трех треугольников 2, 3,4*).

Из рис. 64 ясно, что никакая точка ни в одном из этих трех треугольников не может доминироваться точкой из другого треугольника. Поэтому рассуждения п. 47.4.2 показывают, что V должно удовлетворять в точности следующим требованиям: для части V в каждом из этих треугольников должно выполняться условие (44:Е:с) из

п. 44.7.3, рассматриваемое для этого -

треугольника (вместо всего фундамен- Рис. 63.

тального треугольника, т. е. Е (е0)).

В треугольниках 2, 3, 4 эти условия совпадают с условиями, описанными на рис. 55, 56 для треугольника Т. Поэтому можно повторить дословно все рассуждения пп. 47.5.1-47.5.4, и частями V в треугольниках 2,3, 4

Таблица 26. К рис. 64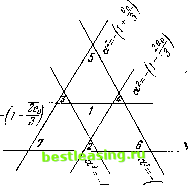

г) Исключая их границы.

2) Включая ее границу.

->-

3) То есть никаким дележом аиз£ (е0). Легко показать, что они не доминируются

->

никаким дележом а вообще - ввиду (45:D) п. 45.2.4 они являются исключенными дележами. Внутренние точки области 1 также не доминируются никакими другими

точками. Иначе говоря, они не доминируются никакими а из Е (е0). Точно так же легко

->

показать, что они не доминируются никаким дележом а вообще - они являются вполне исключенными дележами, см. (45:С) из п. 45.2.4. Эти утверждения можно также проверить непосредственно, используя определения п. 45.2.

4) Оставшаяся часть фундаментального треугольника доминируется границей области 1, которая принадлежит 1.